Разложение уравнения (9.45) в ряд показывает, что оно аппроксимирует ностью до 0(AJC). Разностная схема но если выписать уравнение для всех стема уравнений с трехдиагональной которой могут быть использованы (п. 6.2.2).

Для относительно простого случая можно представить в виде

Тейлора около /-го узла уравнение (9.42) с точ-(9.45) является неявной, узлов, то получается си-матрицей, для решения экономичные способы

точное решение (9.45)

14-0.5/?

1 - 0.5/?

cell J

(9.46)

где Aq и Во выбираются таким образом, чтобы удовлетворялись граничные условия (9.43). Для случая и/а = 20 и Ал: = 0.05, 0.1 и 0.02 решение (9.46) приведено на рис. 9.5. При Дл: = 0.05, что эквивалентно /?ceii = 1, решение довольно хорошо согласуется с точным. При /?се11 = 2 (Дл: = 0.1) решение совпадает с точным везде, кроме пограничного слоя в окрестности л:= 1. Для более грубой сетки при Rceu = 4 решение не только является неточным, но и носит колебательный характер.

Из (9.46) видно, что колебательных решений не будет, если Rceu 2. Полезно также связать поведение решения, показанное на рис. 9.5, с собственными числами матрицы системы уравнений (9.45), записанных с граничными условиями (9.43). Эта система имеет вид

т. е.

b с а b с

АТ = В,

(9.47а)

а b с а b

(9.47b)

где а = -(I-f 0.5/?ceii), b = 2 и с = - (1 - 0.5/?сеп). Собственные числа вышеприведенной трехдиагональной матрицы связаны с а, Ь и с следующими соотношениями:

Я; = 6 + 2 {асУ cos (т), /= 1, 2, ...,/- 2. (9.48)

Видно, что для того, чтобы собственные числа были вещественными, необходимо удовлетворить условию ас 0:

(l-f0.5/?cell)(l-0.5/?ceIl)>0 или /?се11<2. (9.49)

Таким образом, появление осциллирующих решений связано с появлением комплексных собственных чисел.

Для матрицы А в (9.47а) общею вида ограничение на собственные числа X дается теоремой круга Гершгорина (см. [Jennings, 1977])

Таким образом, собственные числа матрицы А лежат в кругах, связанных с каждым рядом матрицы А. Центр каждого круга определяется диагональю с элементами а,/, а радиус- суммой внедиагональных элементов каждого ряда. В работе [Carey, Sepehrnoorl, 1980] применялась теорема круга Гершгорина для анализа уравнений вида (9.47а) при различных значениях jRceii. В интервале О < Rcew 2 центр круга Гершгорина лежит в точке {-2а/Ал:2, 0} комплексной плоскости, имеет радиус 2а/Ал:2 и все собственные числа расположены на отрицательной части вещественной оси. С увеличением Rceiu Т. е. с уменьшением а, радиус круга уменьшается, а центр перемещается к началу координат. При Rcew = 2 центр круга расположен в точке (-и/Ах, 0), радиус равен и/Ах = = 2а/Ах. При Rceu > 2 радиус остается постоянным, но центр движется к началу координат и собственные значения являются комплексными. При Rceu = оо центр круга совпадает с началом координат, а собственные значения становятся чисто мнимыми величинами.

Ограничение jRceii = В для получения неосциллирующих решений применимо и к другим методам, в частности к методу конечных элементов. В работе [Finlayoon, 1989] получено значение В для метода конечных элементов и метода ортогональной коллокации. Однако обычно В меньше 10.

Следует подчеркнуть, что осциллирующие решения могут появиться, если jRceii > В, а появятся ли они на самом деле, зависит от геометрии потока и граничных условий. Например, замедление потока перед препятствием часто порождает осциллирующее решение при ceii > В. Однако для равномерного или ускоряющегося потока можно построить неосциллирующее решение и при Rceu > В.

Как и следовало ожидать, если для представления дТ/дх в (9.42) использовать не центральные разности, а разности против потока (Tj - Tj-i)/Ax, то осциллирующие решения не

-0.5

о Ax=e.2,R , 4 (против потока) >j e-fRcell (центральная) /\

---точное решение

и/к= 2в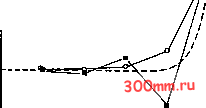

Рис. 9.6. Решение уравнения конвекции - диффузии по схеме с разностями

против потока.

ляции в решении отсутствуют, но решение не является достаточно точным.

Разложение уравнения (9.50) в ряд Тейлора показывает, что оно аппроксимирует (9.42) только с точностью О (Ал:). С точностью 0(Дл:2) (9.50) аппроксимирует уравнение

dT dx

-~а(1 +0.5/?с

(9.51)

т. е. использование разностей против потока приводит к появлению искусственной диффузии O.SjRceiia, аналогично тому, как при использовании конечных разностей против потока для уравнения конвекции тоже возникала искусственная диффузия (см. (9.13)). Практически для получения достаточно точного решения из (9.51) вытекает ограничение 0.5/?сеи<С1, которое является более жестким, чем (9.49).

Если при л: =1.0 вместо условия Дирихле поставить граничное условие Неймана, то характер решения существенно не изменится. Для больших значений uja схема центральных разностей (9.45) приводит к решениям с еще большими осцилля-циями, чем показанные на рис. 9.6.

возникают. Разностная схема со сдвигом против потока дает вместо (9.45) следующий алгоритм:

- (1 + Rceu) +2(1+ 0.5/?cell) Tj -Tj,= 0. (9.50)

Из (9.48) видно, что схема против потока имеет вещественные собственные числа при всех значениях /?ceii. Репиение с использованием разностной схемы против потока для uja = 20 и Дл:=0.2 показано на рис. 9.6. Как и следовало ожидать, осцил-