Глава 10

Нелинейные задачи с преобладающим влиянием конвекции

в гл. 9 были рассмотрены линейные задачи с преобладающим влиянием конвекции. Как было показано там, процесс дискретизации уравнений, и в особенности их конвективных членов, требует особой осторожности во избежание появления фиктивных членов с высшими производными (если иметь в виду модифицированное уравнение), которые по своей величине могут оказаться сравнимыми с членами определяющего уравнения, важными по своему физическому смыслу. Эта проблема особенно серьезна при введении двухточечных разностей со сдвигом вверх по потоку.

Установление связи производных высокого порядка в модифицированном уравнении (п. 9.2.2) с процессами диссипации и дисперсии позволяет построить более точные вычислительные алгоритмы. Например, четырехточечные системы со сдвигом вверх по потоку позволяют избежать чрезмерных осцилляции, связанных с дисперсией (п. 9.3.2 и 9.4.3), без введения нежелательной диссипации, как в случае двухточечной схемы со сдвигом вверх по потоку.

Конвективные члены, входящие в уравнение энергии (п. 11.2.4), являются линейными, если известно поле скоростей. Однако конвективные члены уравнений импульсов (п. 11.2.2 и 11.2.3) существенно нелинейны. В данной главе рассматриваются дополнительные осложнения, связанные с нелинейной конвекцией. Подходящую для этой цели модель обеспечивает одномерное уравнение Бюргерса, так как оно обладает конвективной нелинейностью той же самой формы, что и уравнения Навье -Стокса для несжимаемой жидкости (§ 11.5), и допускает легко вычислимые точные решения для разнообразных комбинаций начальных и граничных условий.

В процессе применения анализа устойчивости по Нейману конвективную нелинейность необходимо нейтрализовать. Эта осуществляется путем временного замораживания коэффициентов при производных, фактически зависящих от решения. При анализе нелинейных вычислительных алгоритмов можно вос- пользоваться методом модифицированного уравнения [Klopfer,.

McRae, 1983J, однако появление произведений производных высшего порядка делает процесс построения схем повышенной точности менее конкретным и надежным (п. 10.1.4), чем это было для линейных уравнений (п. 9.4.3).

Нелинейный характер конвективных членов обусловливает появление больших градиентов зависимых переменных. Это наводит на мысль об использовании неоднородных сеток, локально измельченных в окрестности быстрых изменений решения. Влияние неоднородности сетки на ошибку аппроксимации и точность решения кратко анализируется в п. 10.1.5. Этот вопрос более подробно обсуждается в гл. 12.

Определяющие уравнения гидроаэродинамики (гл. 11) обычно имеют структуру систем, являясь при этом нелинейными. Дополнительные осложнения, связанные с построением вычислительных алгоритмов для систем нелинейных уравнений, подвергаются предварительному рассмотрению в § 10.2.

Как мы видели ранее (гл. 5), метод Галёркина с конечными элементами приводит к точным и экономичным алгоритмам для решения линейных задач с преобладающим влиянием конвекции (п. 9.1.4, 9.4.3 и § 9.5). Однако учет конвективной нелинейности является потенциально неэкономичным в условиях многомерности или при использовании интерполяции повышенного порядка. Недостаточная экономичность может быть преодолена за счет применения группового метода конечных элементов; описание этого метода дается в § 10.3.

Схемы расщепления, рассмотренные в § 8.2, 8.3 и 9.5, распространяются на двумерные уравнения Бюргерса в п. 10.4.2. Как и их одномерный вариант, двумерные уравнения Бюргерса допускают без труда строящиеся точные решения, по крайней мере для предельного стационарного состояния, позволяя тем самым осуществлять прямые оценки точности конкретных вычислительных алгоритмов (п. 10.4.3).

1 § 10.1. Одномерное уравнение Бюргерса

Одномерное уравнение Бюргерса [Burgers, 1948] имеет вид

Уравнение Бюргерса аналогично уравнению переноса (9.56), если не считать того, что здесь конвективный член является уже нелинейным. Это та же самая форма нелинейности, которая имеет место и в уравнениях импульсов (п. 11.2.2 и 11.2.3). Чтобы подчеркнуть упомянутую связь с уравнениями импульсов, коэффициент диффузии а из уравнения (9.56) был заменен

дй . . дй

(10.2)

которое можно сравнить с уравнением (9.2). Наличие нелинейности в уравнении (10.2) позволяет развиваться непрерывным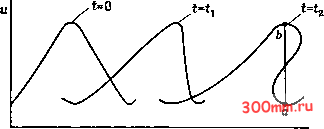

Рис. 10.1. Формирование неоднозначного рещения невязкого уравнения Бюргерса (10.2).

решениям. На рис. 10.1 дается схематическая иллюстрация того, как происходит этот процесс. Конвекция переносит волну слева направо, и на рисунке показаны решения для последовательности значений времени = 0, tu 2. Точки на волне, где значения и больше, подвергаются более быстрой конвекции и в конечном итоге опережают участки волны, конвектируемые с меньшими значениями й. Чтобы уравнение (10.2) имело единственное решение (и приносило результат, имеющий физический смысл), необходимо постулировать возникновение ударной волны (линия аЬ на рис. 10.1), при переходе через которую й изменяется разрывным образом.

Сравнимая с этой схемой эволюция волны для вязкого уравнения Бюргерса (10.1) показана на рис. 10.2. Вязкий член удй/дх производит двоякое воздействие. Во-первых, он уменьшает амплитуду волны при возрастании t (точно так, как и для уравнения переноса). Во-вторых, он предотвращает развитие многозначных решений, подобных показанным на рис. 10.1.

на коэффициент кинематической вязкости v в уравнении (ЮЛ). Более глубокий анализ уравнения Бюргерса проводится в работах [Fletcher, ШЗа; Whitham, 1974].

10.1.1. Физическое поведение

Если из уравнения (10.1) удалить вязкий член, то в результате получим невязкое уравнение Бюргерса