§ 2.3. Параболические дифференциальные уравнения в частных производных

Параболические ДУЧП встречаются при рассмотрении тех задач, где включены некоторые диссипативные механизмы, такие, как вязкостное напряжение или теплопроводность. Классическим примером параболического ДУЧП является уравнение диффузии или уравнение теплопроводности

Уравнение (2.58) будет использовано для демонстрации различных вычислительных методов в гл. 7.

При начальном условии а = sin ял: и граничных условиях и(0, t)=u{l, t)=6 уравнение (2.58) допускает точное решение

и{х, /)=81пяА:ехр(-я20. (2.59)

Экспоненциальное затухание, демонстрируемое формулой (2.59), являет собой контраст в сравнении с осциллирующим решением (2.5) волнового уравнения (2.48).

Уравнение переноса (см. § 9.4 и 9.5) представляет собой линейное параболическое ДУЧП, а уравнение Бюргерса, рассмотренное в § 10.1, является нелинейным параболическим ДУЧП. Однако преобразование Коула - Хопфа (см. [Fletcher, 1983]) позволяет превратить уравнение Бюргерса в уравнение диффузии (2.58), Уравнения Навье - Стокса для неустановившегося течения являются параболическими. Эти уравнения используются как при решении нестационарных задач, так и в тех случаях, когда псевдонестационарная формулировка (см. § 6.4) вводится для решения стационарной задачи. Если иметь в виду строго установившееся течение, то пограничные слои (гл. 15) и сдвиговые слои, как правило, определяются посредством параболических ДУЧП, причем направление потока играет времениподобную роль. Многие из упрощенных вариантов уравнений Навье -Стокса (гл. 16) определяются посредством параболических ДУЧП.

2,3.1. Интерпретация с помощью характеристик

Если интерпретировать уравнение (2.58) как уравнение (2.8), с заменой у = t, то выявляется, что Л = 1, В = С - О, так что уравнение (2.58) оказывается параболическим. Как показывает решение уравнения (2.14), здесь имеется единственное характеристическое направление, определяемое соотношением dt/dx = 0. Характерная вычислительная область для урав-

нения (2.58) представлена на рис. 2.8. В противоположность ситуации, возникавшей для гиперболических уравнений, при переходе через линию t = ti производные функции и всегда остаются непрерывными. Характеристики не играют здесь такой значительной роли, как это было для гиперболических урав-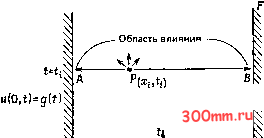

(1,t)=h(t)

х=0 u(x,0)=uote) а;=1

Рис. 2.8. Вычислительная область для параболического ДУЧП.

нений. Для параболических ДУЧП не существует эквивалента методу характеристик. Ясно, что если построить вычислительную сетку, следуя локальным характеристическим направлениям, то никогда не удастся осуществить продвижение решения во времени.

2.3.2. Интерпретация на физической основе

Для параболических задач характерны такие решения, которые реализуют маршевое продвижение во времени, но создают рассеяние в пространстве. Так, например, возмущение решения, введенное в точке Р (см. рис. 2.8), может оказать влияние на любую часть вычислительной области, соответствующую условию t ti. Однако при этом величина возмущения быстро уменьшается по мере удаления от точки Р. В случае установившегося течения в двумерном пограничном слое (гл. 15) характеристики идут по нормали к направлению течения и здесь не создается влияния в направлении вверх по потоку.

Появление диссипативного механизма косвенно указывает также и на тот факт, что даже если начальные условия содержат разрыв, то решение во внутренней области всегда будет оставаться непрерывным. Дифференциальные уравнения в частных производных, определяющие решение более чем в одном пространственном направлении и являющиеся параболическими по-отношению ко времени, становятся эллиптическими в стационарном состоянии (если только стационарное решение существует).

2.3.3. Надлежащие граничные (и начальные) условия

Для уравнения (2.58) необходимо ставить начальные условия Дирихле, например

и (jc, 0) = Uo{x) при О < л: < 1. (2.60)

Надлежащими граничными условиями могут быть

u(0,t) = g{t) и (1,/) = Л(0. (2.61)

На границах CD и EF (см. рис. 2.8) допустима любая комбинация условий Дирихле, Неймана или же смешанных (см. п. 2.1.2). Однако при задании граничных условий Дирихле желательно обеспечить их непрерывную стыковку с начальными условиями в точках С и Е. Невыполнение этого требования приведет к решению, содержащему очень большие градиенты вблизи точек С и £, а это может создать трудности с реализацией вычислительного алгоритма. В случае систем параболических ДУЧП задание начальных условий на линии СЕ и граничных условий на линиях CD и EF необходимо вводить для всех искомых переменных.

§ 2.4. Эллиптические дифференциальные уравнения в частных производных

В гидроаэродинамике эллиптические ДУЧП ассоциируются со стационарными проблемами. Простейший пример эллиптического ДУЧП дает уравнение Лапласа

+ 0, (2.62)

которое определяет потенциальное течение несжимаемой жидкости. При граничных условиях

ф(х, 0)=sinnA:, (л:, 1) = sin ялгехр (-я), ф{0 у) = ф {1 у) = 0

уравнение (2.62) допускает решение

ф {х у) = sin пх ехр (- пу) (2.63)

в области 0л:1, Oyl.

Уравнение Пуассона для функции тока (11.88), определяющее двумерное завихренное течение, является эллиптическим ДУЧП. Как отмечалось выше, стационарное уравнение Навье - Стокса и стационарное уравнение энергии также являются эл-,липтическими уравнениями.