Для эллиптического ДУЧП второго порядка, представленного в форме (2.1), существует важный принцип максимума [Garabedian, 1964]. А именно как максимальные, так и минимальные значения ф должны достигаться на границе OR, если не считать того тривиального случая, когда величина ф постоянна. Принцип максимума полезен для проведения проверки того обстоятельства, что численные решения эллиптических ДУЧП ведут себя надлежащим образом.

2.4.1. Интерпретация с помоиью характеристик

В случае ДУЧП второго порядка, представленного в обшем виде (2.1), о котором известно, что оно эллиптическое, т. е. для него ААС < характеристики будут комплексными и их невозможно показать в вычислительной области (последняя считается вещественной). При рассмотрении эллиптических задач в гидроаэродинамике идентификация характеристических направлений не может оказаться сколько-нибудь полезной.

2.4.2. Интерпретация на физической основе

Наиболее важная особенность, касающаяся эллиптических ДУЧП, состоит в том, что возмущение, внесенное в точке Р (рис. 2.9), оказывает влияние на все другие точки в вычисли-

ч

Заданы (р или дф/дП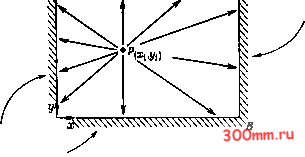

Заданы А (р или д<р/дп

Рис. 2.9. Характерная область для эллиптического ДУЧП.

тельной области, хотя вдалеке от точки Р это влияние будет малым. Тем самым косвенно утверждается, что при попытке отыскания численных решений эллиптических задач необходимо рассматривать глобальную область. В противоположность этому параболические и гиперболические ДУЧП можно решать

прогрессивно-маршевым путем, отталкиваясь от начальных условий. Разрывы в граничных условиях для эллиптических ДУЧП сглаживаются внутри области.

2,4.3, Надлежащие граничные условия

Тот факт, что любая точка внутри области способна оказать влияние на все другие точки рассматриваемой области, влечет за собой вывод о том, что граничные условия необходимо ставить на всех границах (см. рис. 2.9). Граничные условия могут представлять собой любую комбинацию условий Дирихле, Неймана или смешанных (см. п. 2.1.2). Однако если на всех границах поставить условие Неймана dj>ldn = f{s), где символ п соответствует внешней нормали, а s измеряется вдоль контура границы, то необходимо позаботиться о том, чтобы формулировка таких граничных условий не противоречила определяющему уравнению. С помощью теоремы Грина полу- чим

d5=- v<t>dV, (2.64)

dR R

:Ясно, ЧТО если определяющее уравнение представляет собой уравнение Лапласа или уравнение Пуассона, то соотношение (2.64) косвенно указывает на наличие дополнительного гло-бального ограничения, налагаемого на формулировку граничного условия Неймана. Если уравнение (2.62) характеризует установившееся потенциальное течение несжимаемой жидкости, причем ф представляет собой потенциал скорости, то величина f точно соответствует нормальной скорости. Таким образом, в случае установившегося потенциального течения несжимаемой жидкости условие (2.64) совпадает с условием сохранения массы (11.7). Численная реализация условия (2.64) обсуждается в п. 16.2.2. Для систем эллиптических ДУЧП граничные условия должны ставиться на всех границах, для всех искомых переменных.

При рассмотрении параболических и гиперболических ДУЧП путем применения разложения в ряд всегда возможно получить некое локальное решение в непосредственной близости от границы. Попытка проделать то же самое, имея дело с эллиптическим ДУЧП, приводит, как правило, к получению бесконечно возрастающего решения, и это имеет непосредственную связь с тем фактом, что постановка задач для эллиптических ДУЧП оказывается некорректной, если граничные условия не заданы на некоторой замкнутой границе.

§ 2.5. Традиционные методы решения

В данном разделе дается краткое описание трех методов решения, которые могут быть названы прекомпьютерными, так как они требуют только ручных расчетов или расчетов на примитивных машинах. Эти методы хорошо работают применительно к простым модельным задачам, однако оказываются менее эффективными по отношению к более сложным уравнениям, определяющим течение жидкости или газа. Тем не менее иногда эти методы полезны, так как помогают подсказать метод решения или получить некое приближенное или же локальное решение.

2.5.1. Метод характеристик

Этот метод применим только к гиперболическим ДУЧП. Он описывается здесь применительно к ДУЧП второго порядка с двумя независимыми переменными

1> + в + С0 + Я = О. (2.65)

Решение уравнения (2.14) позволит получить два корня

4f- = f и - = 0. (2.66)

Для двух соседних точек на характеристиках, определяемых соотношениями (2.66), условие совместности (2.15) может быть приближенно представлено в виде

A-p + cQ + нy = o. (2.67)

Можно напомнить, что, как это было указано в п. 2.1.3, Р = = ди/дх и Q = ди/ду, и, следовательно, для тех же двух соседних точек

u = px + Qy. (2.68)

Будем предполагать, что и, Р и Q известны вдоль некоторой границы, не являющейся характеристикой (рис. 2.10). На начальном этапе неизвестны ни решение, ни положение таких внутренних точек, как d и е. Из соотношений (2.66) можно получить два соотношения для определения положения точки d. Эти соотношения таковы:

Уа-Уа = Раа(ха-Ха\ (2.69)

Уа-Уь=0,а{ха-Хь1 (2.70)

где

Fad = 0.5 (Fa + Gbd = 0.5 {Gb + G).