По существу, кривые линии ad и bd были заменены здесь прямыми линиями, определяемыми путем осреднения наклона первоначальных линий в концевых точках.

Если величины Ха и уа известны, то из уравнения (2.67) можно найти Pd и Qd с помощью соотношений

АаЛа (Pd - Ра) + Cad (Qd Qa) + Had iVd - У a) = О, (2.71)

AbdGbd {Pd - Pb) + Cbd {Qd - Qb) +bd {yd - Уь) = 0. (2.72)

При известных Pd и Qd можно воспользоваться формулой (2.68), чтобы получить Ud:

Ud-Ua = Pad {d - a) + Qad {yd - У a)-

(2.73)

Ha практике, чтобы получить Xd, yd, Pd, Qd и Ud, уравнения (2.69) - (2.73) следует решать с помощью итераций. В каче-

Of-характеристики

-характеристики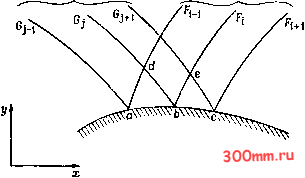

Рис. 2.10. Метод характеристик.

стве начальной итерации используются следующие аппроксимации:

Fad = Fa. Gbd = Gb и т. д. (2.74)

Как правило, если точка d расположена не слишком далеко от а W Ь, достаточно провести две или три итерации. Метод реализует маршевое продвижение вдоль сетки, построенной на локальных характеристиках, определяемых в свою очередь как часть общего решения. Приведенная выше формулироЕка описывается в гидроаэродинамических терминах в работе Бело-церковского и Чушкина [Belotserkovskii, Chushkin, 1965].

Метод характеристик имел широкое применение при исследовании одномерных нестационарных газодинамических задач.

а также при изучении установившегося двумерного сверхзвукового течения невязкого газа. Однако этот метод становится слишком громоздким, если его распространять на случай трех или четырех независимых переменных или если в потоке возникают внутренние ударные волны.

2,5,2, Разделение переменных

Этот метод может применяться к ДУЧП любого типа. Для иллюстрации применения метода рассмотрим уравнение диффузии

Б области, показанной на схеме рис. 2.11. На той же схеме по-

u(0,t)=ON

о \\\\\\\\\\\\\\\\\\\\\\\\\\\\\v u{x,0)=f(x)

Рис. 2.11. Начальные и граничные условия для уравнения (2.75).

казаны начальные и граничные условия. Метод состоит в введении общего расщепленного решения

и(х, t) = X(x)T{t). (2.76)

Подстановка в (2.75) дает

0- + ях=о,

+ яг=о,

(2.77) (2.78)

где X - произвольная постоянная. Уравнение (2.77) имеет бесконечный набор решений вида

Xk{x) = AkSmkx, (2.79)

где Х = k, k = I, 2, 3, ... и Ak - постоянные, определяемые € помощью граничных и начальных условий. Далее, уравнение <2.78) также имеет бесконечное число решений вида

T,{t) = B,exp{-k% (2.80)

где постоянные Bk должны определяться из начальных и граничных условий. Подстановка выражений (2.79) и (2.80) в формулу (2.76) позволяет получить общее решение в форме

и{х, 0=Е CkSinkxexpi-kH). (2.81)

Выражение (2.81) удовлетворяет граничным условиям задачи. Постоянные Ck определяются путем удовлетворения начальным условиям

Е C,smkx = u{x, 0) = /(х), (2.82)

т. е.

Ck =-[fis) sin ksds. (2.83)

По отношению к данной конкретной задаче вклады от множителей exp(-kt) очень малы при больших k и > 0. Поэтому в разложении (2.81) обычно бывает необходимо сохранить лишь 10 или 20 членов.

Принцип разделения переменных связан с возможностью выбора такой системы координат, при которой OR совпадает с координатными линиями. При этом предполагается также, что операторы в ДУЧП могут быть разделены. Отсюда следует, что хотя метод достаточно эффективен при решении модельных задач, он все же нечасто находит прямое применение к решению относительно сложных уравнений, определяющих движение жидкости или газа, при этом нередко в областях неправильной формы. Тем не менее интересное обсуждение данного метода проводится в книге Густафсона [Gustafson, 1920].

2.5.3. Метод функции Грина Для ДУЧП, записанного в обобщенной формулировке

Lu = f, (2.84)

решение в принципе может быть построено путем обращения оператора L. Решение представимо в интегральной форме:

и{р)=\0{р, q)f{q)dV (2.85)

где G(p, (/)-функция Грина. В общем случае функция G{p,q) содержит информацию, эквивалентную информации в операто-