Принципе применена любая методика интегрирования обыкновенных дифференциальных уравнений (см. [Gear, 1971]). Вообще говоря, результат интегрирования можно записать в форме

Т] = Т]+ 5 LaTjdt. (3.13)

Вычисление интеграла в (3.13) по схеме Эйлера дает выражение

Т1 = Т1 + [1аГГМ, (3.14)

тождественное выражению (3.5), если La - конечно-разностный оператор, фигурирующий в уравнении (3.4). Вследствие ошибок, связанных с введением оператора пространственной дискретизации La, использование формулы интегрирования очень высокого порядка для подстановки в (3.13) обычно не дает каких-либо преимуществ. Некоторые из наиболее эффективных алгоритмов решения подобных задач рассматриваются в § 7.4.

§ 3.2. Аппроксимация производных

В § 3.1 были приведены типичные алгебраические формулы, позволяющие проиллюстрировать технику дискретизации производных, подобных дТ/дх. Здесь демонстрируется процесс построения таких алгебраических формул, сначала при помощи разложения в ряд Тейлора, а потом - при помощи некоторой общей процедуры. В каждом случае нетрудно оценить ошибку, обусловленную процессом дискретизации.

3.2,1. Разложение в ряд Тейлора

В качестве первого шага по пути к разработке алгоритма расчета тех значений f, которые могут фигурировать в уравнении (3.1), выразим производные Т по пространству и времени в узле (/, п) через значения Т в близлежащих узлах. Для реализации этого процесса воспользуемся разложениями в ряды Тейлора типа

Эти ряды могут быть оборваны после любого числа членов, причем возникающая в результате ошибка (ошибка аппроксимации) определяется в основном следующим членом разложения, если только Ал: < 1 в разложении (3.15) или если А < 1 в разложении (3.16). Следовательно, можно написать

TUi = T}+Ax

2 L дх if

+ 0(Ajc3). (3.17)

Интерпретация остаточного члена 0(Ал:) сводится к тому, что, как предполагается, существует некоторая положительная постоянная /С, зависящая от Г, такая, что разность между значением Т в узле (/+ 1, и первыми тремя членами правой части (3.17), рассчитанными в узле (/, п) оказывается численно меньше величины КАх для любых достаточно малых Ал:. Ясно, что связанная с такой аппроксимацией ошибка будет быстро уменьшаться по величине по мере уменьшения Ал:.

Обращаясь к выражению (3.17J, нетрудно видеть, что конечно-разностное представление дТ/дх можно получить непосредственно. Действительно, перегруппировка членов в (3.17) дает

= (Г,-Г;)/Ах-0.5Ах[4].+ .... (3.18)

Очевидно, что использование конечно-разностной подстановки

дТ дх Jy

(3.19)

обеспечивает точность О (Ал:). Дополнительные члены, фигурирующие в правой части (3.18), называются в дальнейшем ошибкой аппроксимации. Выражение в правой части формулы (3.19) называется аппроксимацией с разностью вперед. Если разложить величину rf i в ряд Тейлора в узле (/, п) и перегруппировать члены, то можно построить аппроксимацию с разностью назад:

(3.20)

Как и (3.19), эта аппроксимация вносит ошибку О (Ал:). Геометрическая интерпретация выражений (3.19) и (3.20) дается на рис. 3.3. Формула (3.19) оценивает [дТ1дх\} через наклон линии ВС, тогда как формула (3.20) дает ту же оценку посредством наклона АВ.

Формулы (3.19) и (3.20) были получены с помощью разложения в ряд Тейлора по пространству. Разложение в ряд

Тейлора по времени - формула (3.16)-может быть использовано для построения аппроксимации с разностью вперед

рП+\ грп

- (3.21)

L dt Jy

которая вносит ошибку 0(At)j если только предположить, что At < I и что производные высших порядков ограничены.

3.2.2. Аппроксимация оби{его вида

Конечно-разностные выражения, приведенные в п. 3.2.1, были построены с помощью простых перестановок в единственном

Т(Х)р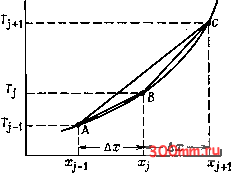

Рис. 3.3. Различные варианты конечно-разностного представления дТ/дх,

разложении в ряд Тайлора. Более последовательная методика построения разностных аппроксимаций сводится к тому, чтобы начать с некоторого общего выражения типа

дТ 1

= аГ; 1 + ЬТ] + cThi + О (Дх ),

(3.22)

где постоянные а, b и с подлежат определению, а член О(Лх) будет указывать на степень точности получаемой аппроксимации.

Используя формулу (3.15), можно написать

аТ1., + ЬТ} + сТ},{а + Ь + с)Т] + (-а + с)Ах

+ {а + с)

Ajc2

дх J/

дх J

+ {-а + с)

L дх J/

1. -f .... (3.23)

Полагая а + 6 + с = О, (-а + с)Ах = 1, получаем а = с - ~ 1/Лх и b = -2с + 1/Ах для любого с. Выбирая с так, чтобы