ВЫСОКОГО порядка, выявляемое на рис. 3.4 и 3.5, зависит еще и от гладкости точного решения. Решения, соответствующие сверхзвуковым течениям невязкой жидкости, могут содержать

Пятиточечная

симметричная схема

, Трехточечная симметричная схема

Разности вперед

1 2,0

0.4 0.8 1.2 1.6 1дйх

Рис. 3.4. Результаты, касающиеся сходимости при вычислении dT/dx; Е = \[dT/dxUI[dT/dxU - 11.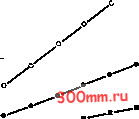

Пятиточечная симметричная у/ схема

Трехточечная симметричная схема

Разности вперед

0,4 0.8 1.2 1.6 Чд Лх

Рис. 3.5. Результаты, касающиеся сходимости при вычислении d4/dx\ Е = \[dT/dx]o/ldT/dx% - 11.

разрывы, связанные с наличием ударных волн (см. [Liepmann, Roshko, 1957]). Если решение оказывается разрывным в пределах того интервала, на котором используются алгебраические формулы, то формула высокого порядка не будет давать

§ 3.3. Точность процесса дискретизации

существенно большую точность. Это можно видеть на примере точного решения, показанного на рис. 3.6.

Использование трехточечной симметричной формулы:

[df/dx] =-0.5/Ах.

Использование пятиточечной симметричной формулы:

[d№L.j =-7/(12 Ах).

Если учесть, что, согласно точному решению, [dT/dx]x=\ = = -оо, то пятиточечная формула не дает заметного преимущества в точности по сравнению с трехточечной формулой.

1.0 X

Рис. 3.6. Разрывное (точное) решение.

Для задач о течении вязкой жидкости при больших числах Рейнольдса (т. е. при малой естественной диссипации) решений с разрывами быть не может, но могут возникать очень большие градиенты. Если градиент достаточно велик, а сетка достаточно грубая, то схемы высокого порядка не приносят преимуществ. Это можно проиллюстрировать на примере функции y = th[k{x-1)], которая представлена графически на рис. 3.7 для трех значений параметра k. Очевидно, что существует градиент, центрированный в точке х=1, величина которого возрастает вместе со значением параметра k. Первая производная dy/dx оценивалась при х = 0.96 с использованием трехточечной и пятиточечной симметричных формул (см. табл. 3.1) для уменьшающихся значений Ах при = 5 и 20.

Результат демонстрируется на рис. 3.8. Нетрудно заметить что пятиточечная формула обеспечивает преимущество в точности только тогда, когда сетка является достаточно мелкой. Требуемая степень измельчения возрастает по мере того, как градиент становится больше (возрастающее значение k). Для некоторых промежуточных значений Ах пятиточечная формула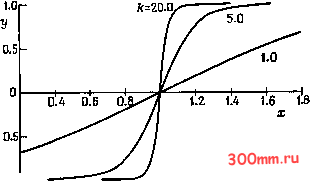

Рис. 3.7. Аналитическая функция у = ih[k(l - х)].

6р 4-

/с=5

<

Пятиточечная ,о симметричная схема

Трехточечная симметричная схема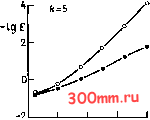

ОЛ 0.8 1.2 1.6 2.0

-1дЛх

/f=20

Пятиточечная симметричная о схема

Трехточечная симметричная

ОЛ 0.8 1.2 1.6 2.0 -1дЛх

Рис. 3.8. Сходимость конечно-разностного значения [dyldx]FD: влияние гладкости решения;

Е = \[dyldxU/[dyldxU - 11.

Пятиточечная симметричная схема

Трехточечная симметричная схема

0.4 0.8 1.2 1.6 2.0

К=20

Пятиточечная симметричная схема

* Трехточечная симметричная схема

0.4 0.8 1.2 1.6 2.0

-IgArr

Рис. 3.9. Сходимость [dy/dxFo: влияние гладкости решения;

Е = lldy/dxhD/midxe. - 11.