Принятие выражения (5.9) эквивалентно тому, чтобы выполнялось требование:

Величина R dx dy dz является наименьшей.

(4) Метод Галёркина.

Wm{x. У. z) = <j>m{, у, г), (5.10>

т. е. весовые функции выбираются из того же семейства, что и аппроксимирующие (пробные) функции. Если аппроксимирующие функции составляют полную систему (в случае полиномов полная система имела бы вид 1, х, л: ..., х), то уравнение (5.5) показывает, что невязка ортогональна к каждому элементу полной системы. Следовательно, по мере того, как М стремится к бесконечности, приближенное решение Т будет сходиться к точному решению 7.

5J.L Приложение к обыкновенному дифференциальному

уравнению

Сравнение различных методов взвешенных невязок можна провести, если построить решение обыкновенного дифференциального уравнения

Ж -у = о при.0<;с<1 (5.11)

с граничным условием у = 1 при л: = 0. Эта задача имеет точное решение у = ехр

Подходящее приближенное решение, эквивалентное выражению (5.2), имеет вид

y=l + Za,xL (5.12)

Это приближенное решение автоматически удовлетворяет граничному условию. В отличие от того, что было в случае (5.2),. коэффициенты а/ в выражении (5.12) постоянны. Подстановка (5.12) в уравнение (5.11) дает невязку уравнения в виде

R=-l + Z aj{jxt--x% (5.13)

Для определения коэффициентов А/ интеграл невязки, взятый с некоторым весом по всей вычислительной области, прирав-

нивается нулю. Следовательно, по аналогии с (5.5) имеем

(5.14)

Различные варианты метода взвешенных невязок реализуются за счет различного выбора весовых функций Wm{x). Например, в методе Галёркина берется Wm{x) = x при т=1, Л. Вычисление интеграла (5.14) при каждом значении т позволяет получить систему уравнений, которую можно представить в виде

SA = D. (5.15)

Здесь вектор А составлен из неизвестных коэффициентов а/. В случае метода Галёркина элемент матрицы S задается в виде

а элемент вектора D - выражением dm = 1/m. Если задать значение = 3, то уравнение (5.15) принимает вид

1/2 1/6

2/3 3/4 5/12 11/20

(5.17)

а решение этого уравнения записывается как

а, = 1.0141, 2 = 0.4225, 3 = 0.2817.

(5.18)

Подстановка (5.18) в приближенное решение (5.12) дает результат

у=1 + 1.0141Х +0.42252+ 0.2817а. (5.19)

Сравнение этого решения с точным решением дается в табл. 5.1.

График изменения ошибки решения при различных значениях N показан на рис. 5.1. Ясно видно, что ошибка решения быстро уменьшается по мере увеличения Л. Как можно видеть из табл. 5.1, среднеквадратичные значения ошибки решения, а также невязки уравнения /?rms, быстро уменьшаются при увеличении Л. В общем случае точное решение задачи неизвестно и, следовательно, ошибку решения невозможно вычислить. Однако оценить невязку уравнения вполне возможно, и это

Таблица 5.1. Решения уравнения dy/dx - у - О по методу Галёркина

дает качественное представление о том, насколько близко данное решение к точному.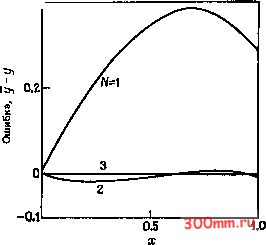

Рис. 5.1. Распределение ошибки для решения уравнения dy/dxу

методу Галёркина.

О по

К решению уравнения (5.11) применялись и некоторые другие разновидности метода взвешенных невязок из числа упомянутых в § 5.1. При = 3 метод наименьших квадратов по-