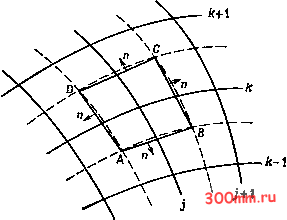Рис. 5.3. Двумерный конечный объем.

Применение метода подобластей к уравнению (5.23) внутри конечного объема ABCD, показанного на рис. 5.3, дает

ABCD

или, если применить теорему Грина,

-±\qdV+ 5 H.nrfs = 0, (5.25)

ABCD

где Н =(f, G). В декартовых координатах имеем

Hnds = Fdy--G dx. (5.26)

Уравнение (5.25) является не чем иным, как KoncTaTauneju консервативности. В частном случае, если выбрать = р, F = pu,

5.2.1. Уравнения, содержашие только первые производные

Здесь мы проиллюстрируем применение метода конечных объемов к решению уравнения первого порядка в общем виде

f-+l-+- .

которое при соответствующем выборе F и G может представлять различные уравнения движения. Например, если положить q = p р = рй и G = pVy то уравнение (5.23) совпадет с двумерным вариантом уравнения неразрывности (11.10).

</ = ру, уравнение (5.25) совпадет с интегральной формулировкой закона сохранения массы. Следовательно, метод конечных объемов сводится к дискретизации исходного уравнения, представленного в интегральной форме (см. § 11.2), в противоположность методу конечных разностей, который обычно применяется к исходному уравнению в его дифференциальной форме.

Одним из приближенных представлений уравнения (5.25) ножет быть уравнение

4гi<1l,k) + Y.{Fy-Gx) = (}, (5.27)

где - площадь четырехугольника ABCD, показанного на рис. 5.3, причем 9/, k есть величина, связанная со средним значением q внутри четырехугольника. В уравнении (5.27)

Уав = Ув- у а, Длв = хв - ха, Fab = 0.5 (F, и-х + /у, k\ Gb = 0.5 (G + G; )

и аналогичные выражения для Аувс и т. д. Если не является функцией времени, то уравнение (5.27) принимает вид

dQf, k/dt + 0.5 (Fy, k-i + k) Уав - 0.5 (G, + G/ ) Ахв + + 0.5 (Fy, k + k) Увс - 0.5 (G/, k + Gy+i, k) хвс + + 0.5 (F/, k + Fj k,) Ay cd - 0.5 (G; + G/, Ac + + 0.5 (F/.i -f F; ) Ау,л ~ 0.5 (G/i + G; ) Axoa = 0. (5.28)

Если глобальная сетка (/, k) является нерегулярной, то записанное для конечных объемов уравнение (5.28) обеспечивает дискретизацию в декартовых координатах, без необходимости введения обобщенных координат (см. гл. 12). Если же глобальная сетка является однородной и ее линии совпадают с линиями постоянных л: и у, то уравнение (5.28) принимает вид

АхАу 4гЯик- 0.5(G/,+ G/ ) Ах + 0.5(F/ + F/i ) Ay + + 0.5 (G/, k + G/, ki) x - 0.5 (F;.i + F/ ) Ay = 0,

rfT +-Ш-+ 2Гу

ЧТО совпадает с аппроксимацией, полученной при представлении пространственных производных в (5.23) с помощью центральных разностей.

Метод конечных объемов, который применялся для описания течения как несжимаемой, так и сжимаемой жидкостей обладает двумя важными преимуществами. Во-первых, он обладает хорошими консервативными свойствами (сохранение массы и т. п.). Во-вторых, он допускает дискретизацию сложных вычислительных областей в более простой, хотя и не обязательно столь же точной форме, чем это позволяет изопара-метрическая конечно-элементная формулировка (см. п. 5.5.3) или введение обобщенных координат (см. § 12.2).

5.2.2, Уравнения, содержащие вторые производные

В п. 5.2.1 метод конечных объемов был приведен к решению уравнения (5.23), содержавшего только первые производные, и привел к сравнительно просто получаемому дискретному выражению (5.28). Если же исходное уравнение содержит вторые производные, то метод конечных объемов нуждается в некоторой модификации.

Эта ситуация будет проиллюстрирована здесь на примере построения решения уравнения Лапласа

# + -g-=0 (5.30)

в вычислительной области, показанной на рис. 5.4, с приводимыми ниже граничными условиями Дирихле:

на WX =0,

Ф== sin в/гху.

<l=\lrrz. (5-31)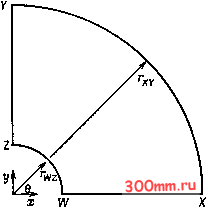

на XY на YZ на ZW

При таком выборе граничных условий уравнение (5.30) имеет точное решение

Рис. 5.4. Вычислительная область для решения уравнения Лапласа.

= (sin е)/г,

(5.32)

наличие которого позволяет непосредственно оценить точность вычислительных решений.

Если бы уравнение Лапласа (5.30) было записано в полярных координатах, то показанная на рис. 5.4 вычислительная область имела бы правильную форму. Однако благодаря