умышленной формулировке задачи в декартовых координатах возникает возможность продемонстрировать способность метода конечных объемов оперировать с областями неправильной формы, сохраняя при этом преимущество легко вычисляемого точного решения. Программа FIVOL (см. п. 5.2.3) имеет достаточно общую форму, позволяющую применить ее к областям других конфигураций, если только предварительно были заданы внутренние узловые точки, например, с помощьк> приема, рассмотренного в п. 13.2-13.4.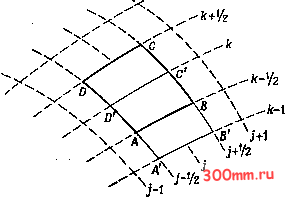

Рис. 5.5. Конечный объем для деформированной сетки.

Следующий этап метода конечных объемов связан с применением метода подобластей к уравнению (5.30) в конечном объеме ABCD, показанном на рис. 5.5, что дает

ABCD

dxdy= J Н -115= О,

(5.33)

ABCD

Н nrfs =

дх ду

Следуя тем же путем, как и в п. 5.2.1, приближенное представ-ление уравнения (5.33) запишем в виде

\.дх\ +

/.k-m l-I/. k-ii2

дф-] . [ дФ1 д i [ дФ

1дх]

дФ

-yh,k+i/2

и 6+1/2

AXcD +

дФ

1дх]:

j-ll2.k

УОА -

дФ ду }f

l-\/2.k

(5.34>

(5.36)

дх г дФ

ABCD

а также аналогичное выражение для

\ fdx.

Если сетка не слишком сильно деформирована, то Аулв - AycD Аул5, Аувс - AyDA Аук-\.к и

Sab = Sabcd = АхАвАук-\. k - АуАвАхк-\, k- (5.37)

На этом основании выражение (5.35) принимает вид

АЛД (/. fe-l - fe) + Afe-l, fe iB - л)

- [Алв (/. fe-l - fe) + Ч-х, k {в - л)]

Если получить аналогичные выражения для [(?/(9л;]/+1/2, й и т. д., то уравнение (5.34) можно записать в виде

Qab {.Фи k-i - Ф1, k) + Рав (Фв - Фа) + Qbc {Ф,+1, k - Фи к) +

+ Рве (Фс - Фо) + QCD (Фи + 1 - Фи k) + PcD {Фо - Фс) +

+ Qda {Ф1-х, k - Фи k) + Pda (Фа - Фа) = О, (5.39)

Яав = {х1в+Уав)15ав> РАВ = {ХАВХк-1.к + УАВУк-1, kVAB

<вс={вс+Увс)/вс PBCiBci+u I + УвсУ1+1. iVbc Ясо={со+Усо)1со PcD={XcDXk+uk + УсоУк+икУсо оа={хоа+у1а)1ол Роа=(хоах,-~1. 1 + УоАУ1-и iVDA

Различные приемы вычисления производных [дф/дх]. j/2 и т. д. рассматриваются в книге [Peyret, Taylor, 1983]. Здесь величина [дф/дх]1 12 вычисляется как среднее значение по площади ВВСЬААВ на рис. 5.5. В результате получим

Фигурирующие в (5.39) значения Фа, ха, Уа вычисляются как средние из четырех узловых значений вокруг данной точки. Так например,

Фа = 0.25 (д ; + </>/-!, + k-x + </>/, k-xY

Подстановка подобных выражений в уравнение (5.39) приводит к следующему девятиточечному дискретному варианту уравнения (5.30):

0.25 (PcD - Pda) /-1, kx + [QcD + 0.25 (Pc - Pda)] Фи k-i + + 0.25 (Psc - Pcd) /41, kx + [Qda +

+ 0.25 {Pcd - Pab)] /-i, k + (Qab - Qbc + Qcd + Qda) Фи k + + [Qbc + 0.25 {Рв - Pcd)] ;41, k +

+ 0.25 {PDA-PAв)ФI-x, k-x + [Qab + 0.25 {Pa - Рве)] Фи fe-i + + 0.25 {Pab - Рве) <t>ix, k-x = 0. (5.40>

Если положение узловых точек сетки определено, то входящие в уравнение (5.40) величины типа Qab, Pab и т. д. могут быть-вычислены раз и навсегда.

Для решения уравнения (5.40) удобно применить последовательную верхнюю релаксацию (ПВР), описанную в § 6.3. Уравнение (5.40) может быть формально разрешено относительно Фл и, следовательно,

г, и = {0-25 {Рсо - Рол) ... + +

+ 0.25 {Рве - Pda) f?. + 0.25 {Рве - Pcd) fi+i, ft+i +

+ [Qda + 0.25 {Pcd - Pab)] Ф1-1, k +

+ [Qbc + 0.25 (Рв - Pcd)] /+.. k +

+ 0.25 {Pda-Pab) h-Uk-1+[Рлв+0.25 {Pda-Pbc)] <l>i,k-i+

+ 0.25 {Рлв - Рве) /+1. k-iV/iQAB + Qbc + Qcd + Qda).

(5.41).

тогда как улучшенное решение выражается в виде

Фк=Ф1.к + {ф1к-ф1к), (5.42).

где К - показатель релаксации (см. § 6.3).

Интересная особенность метода конечных объемов состоит в том, что решение с граничными условиями Неймана (для производных) может быть построено точно так же, как и в случае граничных условий Дирихле, т. е. путем прямой подстановки граничных значений в уравнение (5.34).