гидроаэродинамики используется именно формулировка Галёркина для этого метода. Здесь мы сосредоточимся исключительно на галёркинской формулировке метода конечных элементов.

Традиционная инженерная трактовка метода конечных элементов дается в книге [Zienkiewicz, 1977]. Математические аспекты и перспективы метода более подробно излагаются в-книгах [Strang, Fix, 1973; Oden, Reddy, 1976; Mitchell, Wait, 1977]. Техника вычислений, преимущественно для приложений метода конечных элементов к анализу конструкций, излагается в книге [Bathe, Wilson, 1976]. Приложения традиционного метода конечных элементов к гидроаэромеханике рассматриваются в книгах [Thomasset, 1981; Baker, 1983].

Если сравнивать с традиционным методом Галёркина, изложенным в § 5.1, метод конечных элементов Галёркина обладает двумя чрезвычайно важными особенностями. Сначала приближенное решение (5.2) записывается непосредственно в форме комбинации узловых значений неизвестной функции, т. е.

Г=Е </>/(а:, у, Z). (5.44)

Выражение (5.44) может интерпретироваться как интерполяция по отношению к локальному решению в узловой точке Г/. Благодаря тому что мы работаем непосредственно с узловыми значениями неизвестной переменной, отпадает один уровень в процессе вычислений на этапе решения уравнения (см. гл. 6) и решение в узле приобретает прямой физический смысл. Кроме того, становится легче видеть аналогию с методом конечных разностей, а также становится более очевидной интерпретация метода конечных элементов в качестве средства дискретизации (см. § 3.1) исходного дифференциального уравнения в частных производных, представленного в континуальной форме.

Входящие в выражение (5.44) аппроксимирующие функции /(л:, Уу z) часто называются в математической литературе пробными или интерполяционными функциями, а в инженерной литературе - функциями формы (при замене символа ф/ на Nj), Вторая важная особенность рассматриваемого метода состоит в том, что аппроксимирующие функции /(л:, у, z) выбираются почти исключительно из числа кусочно-линейных полиномов низкого порядка, причем выбор ограничивается ближайшими элементами. Тем самым достигается сравнительно малое число отличных от нуля членов, которые при их надлежащей расстановке [Jennings, 1977, гл. 5] могут располагаться вблизи главной диагонали матрицы уравнений. Это является важным на стадии решения уравнений (см. гл. 6), так как при

подобной ситуации решение матричных уравнений будет более экономичным.

Метод конечных элементов реализует дискретизацию на двух этапах, каждый из которых вносит ошибки (хотя и не всегда аддитивные). На первом из указанных этапов кусочно-линейная интерполяция вводится по дискретным, или конечным, элементам с целью связать локальное решение с узловыми значениями. Этот аспект будет исследован в данном параграфе. На втором этапе используется построение со взвешенными невязками (см. § 5.1), ставящее целью получить алгебраические уравнения для связки между узловыми значениями решения. Техника реализации второго этапа, а также поведение решения иллюстрируются с помощью программ STURM (п. 5.4.2) и DUCT (п. 5.5.2).

5,3,1, Линейная интерполяция

Одномерные линейные аппроксимирующие функции ф]{х) показаны на рис. 5.8. Функция /(л:) принимает значения

/ = 0 при X<Xf..u

/= Г- при Xf ixXf (элемент Л), (5.45)

/=1 при X = Xjy

Ф!=4-г- при XfxXf+i (элементе), (5.46)

/ = 0 при л:>л:у+1.

Таким образом, функция / отлична от нуля только в диапазоне Xji < л: < Xj+i, Подобным же образом можно установить, что аппроксимирующая функция отлична от нуля только между узлами / и / + 2.

В случае линейных аппроксимирующих функций выражение (5.44) принимает вид

Г = Г/.,/.1+Гу/ внутри элемента Л,

Г = Г + Г/+1У+1 внутри элемента 5, \ - )

т. е. благодаря локальному характеру аппроксимирующих функций (см. рис. 5.8) в каждый элемент дают вклады лишь по два члена. Внутри элемента А функция / задается формулой (5.45), а функция /..i - формулой

Внутри элемента В функция задается формулой (5.46), а - формулой

(5.49)

Вышеописанное построение будет использовано для получения линейной интерполяции функции

= 1 + cos (О.бял:) + sin (ял:) (5.50)

в диапазоне О л: 1. Поведение функции, определяемой формулой (5.50), показано на рис. 5.9. Узловые значения опре-

Элемент А Элемент В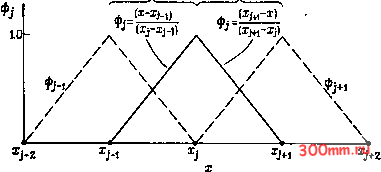

Рис. 5.8. Одномерные линейные аппроксимирующие функции.

деляются с помощью точного решения, т. е. yj = y(Xf). Внутри же конкретного элемента местное решение уш, получаемое путем интерполяции, задается формулами

Уш = У/-1/-1() + Уу/(а:) внутри элемента Л, f/in = y () + f +i</>/+i() внутри элемента В.

(5.51)

Внутри элемента А y i и ф] задаются формулами (5.48) и (5.45) соответственно. Внутри элемента В ф и /+1 задаются с помощью (5.46) и (5.49).

Линейно-интерполяционное решение в форме (5.51) представлено графически на рис. 5.9. Ясно, что при двухэлементном делении интервала О х 1 интерполяционное решение обладает довольно большой неточностью в средних точках каждого элемента, например

X = 0.25: у = 2.63099, ут = 2.35356, jc = 0.75: у = 2.08979, , = 1.85355.