где биквадратные аппроксимирующие функции Лагранжа за-.даются при помощи формул

Угловые узлы: Ф1 (I, ц) = (1 + Ы) ЦЩ (I + Л/Л)-

Узлы в серединах сторон {h = 0): Ф1 {1 ц) = 0.5 (1 -1) цщ (I + цщ).

Узлы в серединах

сторон (Л/ = 0): ф1 (g, ц) = 0.5 (1 - ц) U (1 + Ы).

Внутренний узел: Ф1 (g, т]) = (1 - б) (1 - if).

Как и прежде, квадратичные аппроксимирующие функции Лагранжа обладают интерполяционными свойствами, т. е.

/ = 1, если g = g/, У] = г\1,

ф1 = 0 во всех остальных узлах.

Поведение аппроксимирующей функции (5.62) можно представить зрительно, придавая постоянные значения величинам g или г\; тогда эта аппроксимирующая функция будет вести ч:ебя подобно одномерной аппроксимирующей функции, изображенной на рис. 5.10. Это обстоятельство следует из того факта, что двумерные аппроксимирующие функции Лагранжа .представляют собой просто произведения соответствующих одномерных аппроксимирующих функций. Данный факт дает возможность сделать важные выводы, касающиеся интерполяции в более чем одном измерении, особенно в связи с построением схем, расщепляющихся по размерностям (см. § 8.3).

Двумерная интерполяция на конечных элементах будет .проиллюстрирована здесь по отношению к функции

f = [ 1 - 0.8 cos (0.5ях)] [cos (0.5я(/)], (5.63)

вид которой показан на рис. 5.14 для области -1л:1, -1 {/ 1.

Эту область удобно расщепить на четыре элемента (рис. 5.15), по отношению к которым решение должно интерполироваться билинейным образом при помощи девяти узловых значений fi = f/.

Внутри некоторого конкретного элемента, например С, интер--поляционное решение fin задается в виде

fin== t f 1Ф1 (К Ц), (5.64)

где (g, т])-локальная координатная система, связанная с элементом. Для элемента С имеем

g = 2A:-1 и Т1 = 2г/-1.

Билинейные интерполяционные функции fi задаются формула-ми (5.60), а чаще -формулами (5.59).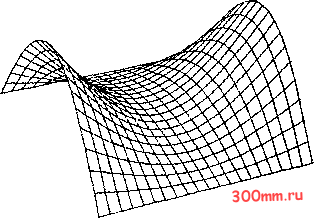

Рис. 5.14. Двумерная функция f = [1 - 0.8 cos (0.5ях)][со8(0.5яг/)].

у=1.0

► у=0

г/=-1.0

Рис. 5.15. Линейные элементы в двух измерениях.

Интерполяционное решение всего с четырьмя элементами является не очень точным. Например, в точке х = 0.5, у = 0.5

f = 0.45711, /in = 0.375.

Целиком интерполяционное решение для функции (5.63) показано на рис. 5.16. Однако точность решения быстро возрастает по мере увеличения числа элементов, покрывающих область

(табл. 5.7). Показанные в табл. 5.7 результаты, относящиеся к билинейной интерполяции, свидетельствуют о том, что среднеквадратичная ошибка уменьшается пропорционально Да:

Таблица 5.7. Ошибки в случае двумерной конечно-элементной интерполяции

Более точная интерполяция может быть достигнута за счет применения биквидратичной интерполяции. Тогда каждый эле-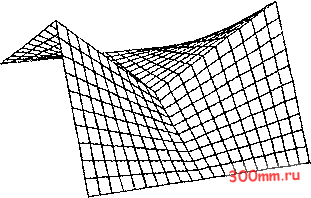

Рис. 5.16. Билинейная интерполяция функции (5.63).

иент имеет девять узловых значений (см. рис. 5.13), которые интерполируются с помощью выражения

/in =Е </>/(?, Л), (5.65)

где интерполяционные функции /(g, т]) задаются с помощью формул (5.62). Как видно из табл. 5.7, элементы с биквадра-