(теплопроводности)

дТ дЧ

(5.90)

в интервале О л: 1 и 0. Предполагается, что начальное условие имеет форму Т{х, 0)=То{х), а граничные условия записываются в виде Г (О, О = а и t) = 6.

Введение тех же самых линейных аппроксимирующих функций (5.70), которые использовались в задаче Штурма -Лиувилля, и такой же способ применения метода Галёркина с конечными элементами дают на однородной сетке следующий результат для внутренних узлов:

Ldt J

dT 1 1

ir\f б

(5.91)

Для указанных выше граничных условий Дирихле не требуется вводить дискретизированные уравнения у граничных узлов.

С учетом того что конечно-элементная формулировка применяется только к пространству, член dT/dt в уравнении (5.90) подвергается такой же обработке, как и непродифференциро-ванный (по пространству) член У в уравнении (5.66). Не удивительно поэтому, что в (5.91) и (5.83) появляются одни и те же весовые множители (1/6, 2/3, 1/6). Если dT/dt заменяется яа AT-y/At, а последний член в левой части уравнения (5.91) вычисляется как средневзвешенная величина по отношению к п-му и (д -- 1)-му слоям по времени, т. е. так, как в уравнении (7.24), то результат принимает форму

е\ At / 34 у бЧ J

fii-f){TU-2T + T],) , {т:{-2Т- + тХ\)Л

V аР Ах )~

(5.92)

где параметр р регулирует степень неявности. Уравнение (5.92) можно представить в следующей компактной форме:

= а [(1 - Р) L..r? + pLrr] = О, (5.93)

где ДГ/ * =Г/ *- Г/ и массовый, и разностный операторы Мх и Lxx определяются соответственно формулами

Мх = {ф, 2/3, 1/6), Lxx = {\ll\ -2/Ax2, 1/Ал:2).

Сравнение с неявной конечно-разностной схемой (7.24) показывает, что единственная разница между ними состоит в том что член с производной по времени в конечно-элементном варианте разбит на слагаемые, определяемые в соседних узлах. Уравнение (7.24) может быть приведено к форме уравнения (5.93), если дать следующее определение массового оператора:

М = (0, 1, 0).

Подобие структуры уравнения (5.93) и уравнения (5.90), послужившего его прообразом, наталкивает на мысль о том что метод конечных элементов можно интерпретировать как почленный процесс дискретизации наподобие конечно-разностного метода. Такая интерпретация изучается в приложении А.2 и используется в § 8.3.

После перестановки членов уравнения (5.93) можно получить неявный алгоритм

{Мх - ШЬхх) ТГ = [Мх + Ш (1 - р) и,] Т1 (5.94)

Важность структуры соотношения (5.94) можно лучше оценить после прочтения § 7.2. Многократное применение соотношения (5.94), центрируемого в каждом из узлов по очереди, позволяет получить трехдиагональную систему уравнений, которую можно решить с помощью алгоритма Томаса (см. п. 6.2.2).

Как будет видно далее, приравнивание р = О в случае конечно-разностной схемы (7.24) приводит к явному алгоритму. Это не так в случае рассматриваемой схемы вследствие неявного характера оператора Мх. Однако благодаря симметричной природе операторов Мх и Lxx, из соотношения (5.94) все же можно получить явную схему, если сделать специальный выбор А = Ах2/(6аР).

Соотношение (5.94) согласуется с уравнением (5.90) при ошибке усечения 0(А<2, Ал:), если р = 0.5, и обладает безусловной устойчивостью, если р 0.5. При специальном выборе Р = 0.5 соотношение (5.94) было применено к анализу примера, рассмотренного в п. 7.2.5; результаты анализа приведены в табл. 7.6.

5.5.2. DUCT: течение вязкости жидкости в канале прямоугольного сечения

Здесь метод конечных элементов будет использован с цельк> представления в дискретной форме характерной двумерной задачи. Полностью развитое ламинарное течение вязкой жидкости в канале прямоугольного сечения (рис. 5.21) определяется

уравнением импульсов в проекции на ось z\

где осевая скорость w{x, у) должна быть определена при заданном градиенте давления dpjdz и заданной вязкости (i.

С точки зрения вычислений целесообразно привести (5.95) к безразмерной форме путем введения величин

Xnd -

1, - ynd - -

Тогда уравнение (5.95) принимает вид (индекс nd опущен)

ZT Г

+ 1=0

(5.97)

граничными условиями

w = Q при

х = ± 1, у = ± 1.

(5.98)

Следуя процедуре наподобие той, которая в п. 5.4.1 применялась к уравнению Штурма - Лиувилля, для w вводится

пробное решение вида

w=Yum<li{x. у). (5.99)

где i[x, у)-двумерные интерполяционные функции, как правило, определяемые формулами, эквивалентными (5.60) или (5.62). Для данной задачи на каждом из элементов будут введены билинейные интерполяционные функции по схеме, представленной на рис. 5.15. Подстановка выражения (5.99) в уравнение (5.97), применение галёркинской формулировки в виде (5.5) и (5.10) и некоторые простые перестановки приводят к следующей системе алгебраических уравнений: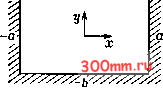

Рис. 5.21. Течение вязкой жидкости в канале прямоугольного сечения.

BW=G,

(5.100)

где компонентами вектора W являются неизвестные узловые значения wi, фигурирующие в (5.99), тогда как элементами матрицы В являются выражения

1 1

\2 дфь дФт дФ1 дФт

дх дх

-1 -1

ду ду .

dxdy, (5.101)