На практике решение строится путем релаксации с последующей переброской на более грубую сетку точного решения на самой грубой сетке, а затем релаксации и пролонгации на все более мелкие сетки по аналогии со схемой, показанной на рис. 6.21. Как только получено решение У , рассчитывается поправка

которая затем пролонгируется на (т+ 1)-ю сетку. После этого подправленное решение, т. е. V * +/W , релаксируется в основном так же, как и в линейном случае, чтобы получить

Схему решения нелинейной задачи называют методом пол-ной аппроксимационной памяти (ПАП) [Brandt, 1977] в отличие от метода поправочной памяти (ПП), описываемого на рис. 6.21. Если учесть, что метод ПАП перебрасывает на более грубые сетки и решение, и невязку, то его экономичность немного ниже (на 5 % - 10 %), чем у схемы ПП; в общем случае метод ПАП не должен использоваться при решении линейных задач. Как и в случае метода ПП, эффективность этого метода зависит от возможности сглаживания поправки к решению W и невязки R.

Описание методов ПП и ПАП было начато с аппроксимации решения на наиболее мелкой сетке, т = М, проходило через V-цикл вплоть до самой грубой сетки и возвращалось обратно, чтобы улучшить начальное решение. Такая стратегия является вполне подходящей, если в нашем распоряжении имеется хорошее приближение к решению V.

Если никакой информации о решении нет, то лучше начинать с решения на наиболее грубой сетке, полученного либо непосредственно, либо с помощью обычных итераций. Для улучшения решения с помощью интерполяции высокого порядка делается переход на следующий уровень более мелкой сетки, а затем проводятся г многосеточных V-циклов. Процесс интерполяции высокого порядка в сочетании с г многосеточными V-циклами повторяется на последовательности все более мелких сеток вплоть до т = М, а многосеточный V-цикл повторяется до достижения сходимости.

Описанное выше составляет основу полного многосеточного метода (ПМС), представляющего собой обобщение методов ПАП и ПП. Схема метода ПМС показана на рис. 6.22 для случая линейной системы уравнений. Функция INT(V , т) символизирует кубическую интерполяцию сначала в направлении jc.

Решить AV = точно m = t

т= m+l г = О

г=г+1 I

а затем для всех узловых значений а:( +> в направлении у. Функция МОЦУ А , В ) соответствует одному проходу через многосеточный V-цикл, показанный на рис. 6.21.

Многосеточный подход можно рассматривать как прием ускорения, подобный методу сопряженных градиентов (п. 6.3.4) и примененный к основной итерационной схеме (п. 6.3.1- 6.3.3.). Другой вариант интерпретации состоит в том, что основная итерационная схема рассматривается как средство сглаживания в рамках многосеточного метода, так же как она рассматривалась в качестве предварительного кондиционера по отношению к методу сопряженных градиентов. Как и при ускорении по методу сопряженных градиентов, было найдено, что использование неполной (приближенной) линейной факторизации матрицы А, переводимой в L-U, весьма эффективно в качестве сглаживающего процесса для соотношений (6.84) и (6.87) [Sonneveld et al., 1985]. Это особенно справедливо в случаях матриц А с сильной асимметрией, например для задач с преобладающим влиянием конвекции (гл. 9 и 10).

Подробное описание многосеточных методов дается в Рис. 6.22. Блок-схема для метода трудах [Brandt, 1977; Stuben, ПМС. Trottenberg, 1982; Hackbusch,

1985], а также некоторых других авторов. Брандт, а также Штубен и Треттенберг приводят написанные на языке Фортран программы по применению простого многосеточного метода к решению уравнения Пуассона. Описание, данное здесь, следует в основном Штубену и Троттенбергу. Приложения многосеточных методов к решению задач о невязком течении приводятся в п. 14.2.9 и 14.3.5, а к проблемам течения вязкой несжимаемой жидкости-в п. 17.2.3 и 17.3.1.

V = MG1 (V U ,B)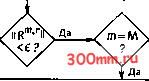

Решение уравнения AV -

пользуясь центрированными конечно-разностными формулами при Ал: = Ау, то метод Якоби дает для внутренних узлов (на сетке /, k типа, показанного на рис. 6.21) выражение

= 0.25 + + vfl к + vf\ (6.93)

Желая получить эквивалентное нестационарное уравнение, следует заменить (6.92) на выражение

Дискретизация с помощью конечно-разностных формул при Ал: = А(/ приводит к алгоритму

tk = (1 - 45) vl k + 5{vl,+1 + vlk-x + k + v]:u k), (6.95)

где s = aAt/Ax. Выбор 5 = 0.25 воспроизводит формулу (6.93). Таким образом, имеется очевидная связь между нестационарной формулировкой и методом итераций, рассмотренным в § 6.3.

Важное преимущество нестационарной формулировки состоит в том, что она позволяет воспользоваться различными приемами расщепления, обсуждаемыми в § 8.2. Например, уравнение (6.94) при его решении по методу НПН приводит к алгебраическим уравнениям (8.14) и (8.15). Решение этих уравнений строится путем решения подсистем уравнений, связанных с каждой из сеточных линий, с помощью алгоритма Томаса (п. 6.2.2). Этот процесс иллюстрируется на рис. 6.23.

Если учесть, что само нестационарное решение интереса не представляет, обычно целесообразно выбрать такую последовательность шагов по времени, чтобы минимизировать общее число временных шагов, необходимое для достижения сходимости. Вид упомянутой последовательности зависит от самой задачи, однако, как правило, имеет характер геометрической прогрессии, причем диапазон изменения временных шагов соответствует диапазону собственных значений, связанных с трехдиаго-

§ 6.4. Псевдонестационарный метод

Альтернатива решению алгебраических уравнений, возникающих при дискретизации некоторой стационарной задачи, состоит в построении эквивалентной нестационарной задачи и решении этой задачи маршевым методом вплоть до достижения стационарного состояния. В подобных условиях время играет роль итерационного параметра.

Таким образом, если провести дискретизацию уравнения Лапласа

+S = 0, (6.92)