Глава 7

Одномерное уравнение диффузии

Если говорить о перспективах развития вычислительных методов, то уравнение диффузии содержит тот же самый дисси-пативный механизм, который обнаруживается при изучении задач гидроаэродинамики со значительным влиянием вязкости или теплопроводности. Следовательно, приемы численного анализа, эффективные для уравнения диффузии, позволят целенаправленно выбрать и надлежащие алгоритмы для решения задач динамики вязкой жидкости (см. гл. 15-18).

В данной главе одномерное уравнение диффузии будет использовано для того, чтобы на примерах его решения разрабатывать явные и неявные схемы. При этом будет уделяться внимание вопросам устойчивости и точности различных схем. Будет рассмотрена также и проблема точного учета граничных и начальных условий.

Ранее (см. § 2.3) мы вводили уравнение диффузии или уравнение теплопроводности

в качестве примера параболического дифференциального уравнения в частных производных, а также пользовались им для иллюстрации процессов дискретизации (§ 3.1) и применения конечно-разностного метода (§ 3.5.

В уравнении (7.1) величина f может рассматриваться как скорость, завихренность, температура или концентрация в зависимости от того, рассматриваем ли мы диффузию импульса, вихря, тепла или массы. Если f - температура, то уравнение (7.1) определяет поток тепла в стержне, который теплоизолирован на боковой поверхности, но может передавать тепло окружающей среде через свои концы (точки Л и В на рис. 7.1).

Обычно встречаются два типа граничных условий. Во-первых, зависимая переменная задается как известная функция времени. В обозначениях уравнения (7.1) такое задание имеет форму (для точки А)

Г (О, 0 = 6(0. (7.2>

То И

Задано \NNSN\<WtennoM3onfluMn 4\\n\\\\\\\\

Задано Г1ли

х=0 а;=1

Рис. 7.1. Одномерный нестационарный процесс теплопроводности.

Для получения единственного решения уравнения (7.1) необходимо задать также и начальные условия. Это может быть сделано в форме

Т{х, Q) = T,{x). (7.4)

Точное решение Т{х, t) удовлетворяет уравнению (7.1), а также условиям (7.4) и (7.2) или (7.3), применяемым при л: = О и jc = 1.0.

С целью построения приближенного решения уравнение (7.1) подвергается дискретизации (§ 3.1), и полученное алгебраическое уравнение приводится к такой форме, которая позволяет составить алгоритм. Этот алгоритм дает возможность получить решение на (M-fl)-M временном слое (см. рис. 3.2) по данным о решении, известном на м-м и на более ранних временных слоях. Описание процедуры в целом дается в § 3.5.

§ 7.1. Явные методы

При использовании явных методов единственная неизвестная, например фигурирует в левой части алгебраической формулы, полученной в результате дискретизации.

Это - граничное условие Дирихле (см. п. 2.1.2). На практике b часто является константой. Во-вторых, можно задать пространственную производную зависимой переменной. Применительно к (7.1) это можно записать в виде (для точки А)

1(0,0 = 0. (7.3)

Это - граничное условие Неймана (см. п. 2.1.2). Как и в случае граничного условия Дирихле, величина с часто является константой.

7.LL Схема ВВЦП

Если для производной по времени ввести двухточечную разностную аппроксимацию со сдвигом вперед, а для пространственной производной - точечную аппроксимацию с центральной разностью, то уравнение (7.1) приобретает следующую форму:

-Xt---aF-=

Уравнение (7.5) будет в дальнейшем называться схемой ВВЦП (разности со сдвигом вперед по времени и центральные

(7.5)

П о-

ВВЦП

j-1 j j+1

Ричардсон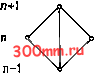

Дюфорт -Франкел

П+1 <

П о-

J-1 j

J-l j j+1 Крлнк-Николсон ТСЧН

Рис. 7.2. Активные узлы в алгебраических схемах для уравнения диффузии.

Линейный МКЭ, Кранк -Николсон

ПО пространству). Как можно видеть, пространственная производная была аппроксимирована на п-м слое по времени, т. е. на известном временном слое. Несколько преобразуя уравнение (7.5), получим алгоритм

ТГ = + (1 - 25) г? 4- sTUu (7.6)

где фигурирует параметр дискретизации 5 = cxAt/Ax.

Узлы сетки, связанные зависимостью по формуле (7.6), показаны на рис. 7.2. Подстановка в уравнение (7.5) функции Г, т. е. точного решения уравнения (7.1), и разложение каждого из членов в ряд Тейлора относительно узла (/, п) (так же, как в п. 3.2.1) дает

J-f £/ = 0,

L dt