Независимо от того, рассматриваете ли Вы Землю как сферу или как сфероид, Вы должны преобразовать ее трехмерную поверхность в плоское изображение на карте. Это преобразование, выполняемое по математическим законам, называется картографической проекцией. Одним из простых способов понимания того, как картографические проекции изменяют пространственные свойства, является визуализация проекции света сквозь Землю на поверхность, которая называется проекционной поверхностью.

Представьте себе, что поверхность Земли прозрачна, и на ней нанесена картографическая сетка. Оберните кусок бумаги вокруг Земли. Источник света в центре Земли отбросит тени от сетки координат на кусок бумаги. Вы можете теперь развернуть бумагу и положить ее на плоскость. Форма координатной сетки на плоской поверхности бумаги очень отличается от ее формы на поверхности Земли. Проекция карты исказила картографическую сетку.

Разложить сфероид на плоскость нисколько не легче, чем расплющить кусок апельсиновой кожуры- он будет разорван. При отображении Земной поверхности в двухмерном пространстве искажается форма, площадь, длина или направление объектов.

Картографические проекции используют математические формулы, определяющие связь между сферическими координатами точек на поверхности эллипсоида или шара и соответствующими координатами точек на плоскости карты.

Различные проекции имеют разные типы искажений. Некоторые проекции разработаны с учетом минимизации искажений одной или двух характеристик данных. Проекция может сохранять площадь объектов, но изменять их форму. На графике, представленном ниже, объекты, расположенные у полюса, вытянуты. Диаграмма на следующей странице показывает, как трехмерные объекты сжимаются для того, чтобы их можно было поместить на плоскую поверхность.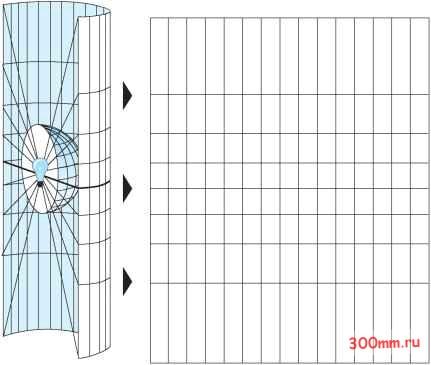

Картографическая сетка географической системы координат, спроецированной на цилиндрическую поверхность.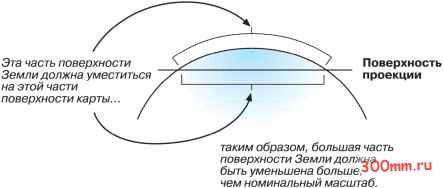

Картографические проекции предназначены для определенных целей. Одни картографические проекции могут использоваться для отображения крупномасштабных объектов на ограниченной площади, другие - для составления мелкомасштабных карт мира. Картографические проекции, используемые для мелкомасштабных, карт обычно основываются на сферической, а не сфероидальной географической системе координат.

Равноугольные проекции

Равноугольные проекции сохраняют без искажений малые локальные формы. Для сохранения отдельных углов, описывающих пространственные отношения, равноугольная проекция должна также представлять линии картографической сетки пересекающимися под углом 90° на карте. Это достигается в этой проекции с помощью сохранения всех углов. Недостаток заключается в том, что площадь, ограниченная рядом кривых, может быть в процессе преобразования значительно искажена. Ни одна из картографических проекций не может сохранять большие территории без искажения формы.

Равновеликие проекции

Равновеликие проекции сохраняют площадь изображаемых объектов. Вследствие этого другие свойства: форма, углы, масштаб - искажаются. В равновеликих проекциях параллели и меридианы могут не пересекаться под правильными углами. В некоторых случаях, особенно на картах небольших территорий, искажение форм не является очевидным, и очень трудно отличить равноугольную проекцию от равновеликой, если только она не была соответствующим образом определена по документации или путем измерений.

Равнопромежуточные проекции

Карты с равнопромежуточными проекциями сохраняют расстояния между определенными точками. Правильный масштаб не сохраняется никакой проекцией на всей карте; однако, в большинстве случаев существует одна или более линий на карте, вдоль которых масштаб сохраняется постоянн1м. В большинстве равнопромежуточнгх проекций есть одна или несколько линий, длина которых на карте равна (в масштабе карты) длине соотносимой с нею линии на глобусе, независимо от того, является ли эта линия большой или малой окружностью, прямой или кривой линией. О таких расстояниях говорят, что они истинные. Например, в Синусоидальной проекции экватор и все параллели имеют свою истинную длину. В других равнопромежуточных проекциях могут быть истинными Экватор и все меридианы. Иные проекции (например, рав-нопромежуточная проекция двух точек) показывают истинный масштаб между одной или двумя точками и каждой другой точкой на карте. Необходимо иметь в виду, что ни одна проекция не бывает равнопромежуточной по отношению ко всем точкам на карте.

Проекции истинного направления

Кратчайший путь между двумя точками на сферической поверхности, такой как поверхность Земли, пролегает вдоль сферического эквивалента прямой линии на плоской поверхности. Это большая окружность, на которой лежат две точки. Проекции истинного направления, или азимутальные проекции, используются для сохранения некоторых кривых, описывающих большие окружности, и придают правильные азимутальные направления всем точкам на карте относительно центра. Некоторые проекции этого типа являются также равноугольными, равновеликими или равнопромежуточными.

Поскольку карты являются плоскими, в качестве вспомогательных поверхностей некоторых простейших проекций используются геометрические фигуры, которые можно развернуть на плоскость без растяжения их поверхностей. Они называются развертывающимися поверхностями. Типичными примерами являются конусы, цилиндры и плоскости. Картографические проекции систематически проецируют местоположения с поверхности сфероида на условные местоположения на плоской поверхности, используя уравнения картографических проекций.

Первым шагом при проецировании одной поверхности на другую является создание одной или более точек контакта. Каждая такая точка называется точкой касания. Как будет показано ниже в разделе Азимутальные проекции (проекции на плоскость) , азимутальная проекция проходит по касательной к глобусу только в одной точке. Конусы и цилиндры касаются глобуса вдоль линии. Если поверхность проекции пересекает глобус вместо того, чтобы просто коснуться его поверхности, то полученная в результате проекция является секущей, а не касательной. Независимо от того, является ли контакт касательным или секущим, его место очень значимо, поскольку определяет точку или линии нулевого искажения. Эту линию истинного масштаба часто называют стандартной линией. В общем случае, искажение проекции увеличивается с увеличением расстояния от точки контакта.

Многие обычные картографические проекции можно классифицировать в соответствии с используемой для них проекционной поверхностью: конические, цилиндрические или азимутальные (проекции на плоскость).