
 |
|
Читаемые статьи
Читаемые книги
Ссылки
|
Главная > Ортографическая проекция Конические проекции Самая простая коническая проекция проходит по касательной к глобусу вдоль линии широты. Эта линия называется стандартной параллелью. Меридианы проецируются на коническую поверхность, сходясь на вершине или в точке конуса. Параллели проецируются на коническую поверхность как кольца. Конус затем рассекается вдоль любого меридиана для создания конечной конической проекции, в которой имеются прямые сходящиеся меридианы и параллели, представленные концентрическими окружностями. Меридиан, противолежащий линии сечения, становится центральным меридианом. Более сложные конические проекции соприкасаются с поверхностью глобуса в двух местах. Эти проекции называются секущими коническими проекциями и определяются двумя стандартными параллелями. Характер искажений при секущих проекциях различается для районов, расположенных между стандартными параллелями, и для районов, расположенных за их пределами. Как правило, секущая проекция дает меньшее суммарное искажение, чем касательная проекция. В еще более сложных конических проекциях ось конуса не совпадает с полярной осью глобуса. Такие проекции называются косыми. 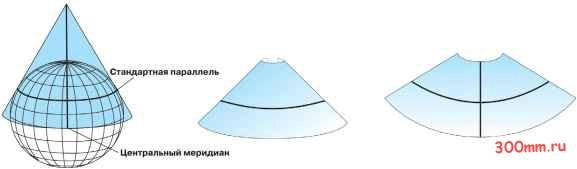 В целом, чем дальше от стандартной параллели, тем больше искажение. Соответственно, отсечение верхушки конуса создает более точную проекцию. Этого можно достичь, если не использовать полярную область при проецировании объектов. Конические проекции используются для среднеширотных зон, имеющих ориентацию с востока на запад. Изображение географических объектов зависит от расстояния между параллелями. При их равном удалении друг от друга проекция получается равнопроме-жуточной в направлении с севера на юг, но не равноугольной и не равновеликой. Примером такого типа проекций является Равнопромежуточная Коническая проекция. Для небольших областей общее искажение минимально. На Конической Равноугольной проекции 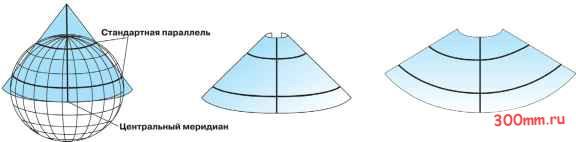 Ламберта расстояние между центральными параллелями меньше, чем у параллелей ближе к границам, и не искажаются формы малых географических объектов на мелкомасштабных и крупномасштабных картах. На Равновеликой Конической проекции Альберса параллели вблизи северного и южного полюса расположены ближе друг к другу, чем центральные параллели, и проекция отображает эквивалентные площади. Цилиндрические проекции Подобно коническим проекциям цилиндрические проекции могут также быть касательными или секущими. Проекция Меркатора является одной из наиболее простых цилиндрических проекций, и экватор обычно является ее линией касания. Меридианы проецируются геометрически на цилиндрическую поверхность, а параллели проецируются математически. При этом создается координатная сетка с углами 90°°. Цилиндр рассекается вдоль любого меридиана для получения конечной цилиндрической проекции. Меридианы расположены через равные интервалы, в то время как интервал между параллельными линиями широты возрастает по направлению к полюсам. Эта проекция является равноугольной и показывает истинное направление вдоль прямых линий. В проекции Меркатора прямыми линиями являются линии румбов - линии постоянного азимута, а не большинство больших окружностей. При создании более сложных цилиндрических проекций цилиндр вращают, изменяя, таким образом, линии касания или сечения. Поперечные цилиндрические проекции, такие как Поперечная проекция Мерка-тора, используют меридианы как линии касательного контакта или линии, параллельные меридианам, как линии сечения. Стандартные линии располагаются в направлении север-юг, и вдоль них масштаб является истинным. Наклонные цилиндры вращают вокруг ли- нии большой окружности, расположенной где-нибудь между экватором и меридианами. В этих более сложных проекциях большинство меридианов и линий широты больше не являются прямыми. Во всех цилиндрических проекциях линия касания или линии сечения не имеют искажений, и, таким образом, являются линиями равных расстояний. Другие географические свойства варьируют в зависимости от конкретной проекции. 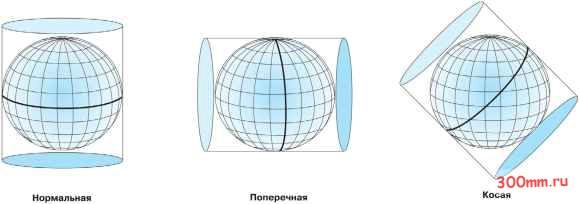
|
 Чем хороши многотопливные котлы?  Нетрадиционное отопление  Детище отечественной Оборонки  Что такое автономное индивидуальное отопление?  Использование тепловых насосов  Эффективное теплоснабжение для больших помещений  Когда удобно применять теплые полы |
|
© 1998 - 2025 www.300mm.ru.
При копировании материала обязательно наличие обратных ссылок. |