Географические преобразования

В этой главе обсуждаются различные методы преобразований датумов, включая:

Геоцентрический сдвиг

Использование системы координат и

радиус-вектора

Метод Молоденски и сокращенный

метод Молоденски

Методы NADCONи HARN

Преобразование для национальных

датумов (США) версия 2 (NTv2)

Методы географических преобразований

Перемещение ваших данных между системами координат иногда включает преобразования между географическими системами координат.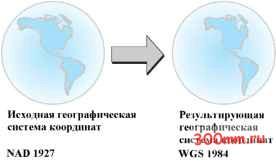

Поскольку географические системы координат содержат датумы, основанные на сфероидах, географическое преобразование меняет также лежащий в основе датума сфероид. Существует несколько методов, которые имеют различные уровни погрешности, для выполнения преобразований между датумами. Точность конкретного преобразования может меняться от сантиметров до метров в зависимости от метода и от качества и числа контрольных точек, используемых для определения параметров преобразований.

Географическое преобразование всегда конвертирует географические (широту - долготу) координаты. Некоторые методы переводят географические координаты в геоцентрические (X,Y,Z) координаты, преобразуют координаты X,Y,Z, и приводят новые значения обратно к географическим координатам.

Преобразования включают методы геоцентрического сдвига, метод Молоденски и метод системы координат.

Другие методы, такие как NADCON и NTv2 используют гриды разницы и конвертируют значения широты-долготы напрямую.

Географическое преобразование всегда определяется с направлением. Параметры трансформации описывают процесс преобразования входной географической системы координат в выходную. Все поддерживаемые методы являются обратимыми. Выполнив географическое преобразование, вы можете провести обратное преобразование. Как правило, приложения автоматически выполняют преобразования в нужном направлении. Например, если вы хотите преобразовать данные из WGS 1984 в Adindan, но в списке доступных трансформаций представлено преобразование Adindan To WGS 1984, вы можете выбрать это преобразование, и оно будет корректно применено.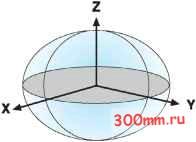

Система координат X,Y,Z.

Методы, использующие три параметра

Простейший метод преобразования датумов - это геоцентрическое преобразование по трем параметрам. Геоцентрическое моделирование моделирует разницу между двумя датумами в системе координат X,Y,Z. Для одного датума центр определяется в точке с координатами 0,0,0. Центр другого датума определяется на некотором расстоянии в метрах (DX,DY,DZ) от этой точки.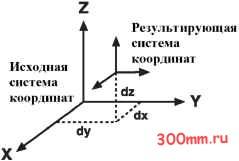

Обычно параметры трансформирования определяются как переход от местного датума к WGS 1984 или другому геоцентрическому датуму.

Три параметра являются линейными сдвигами и всегда выражаются в метрах.

Методы, использующие семь параметров

Более сложное и точное преобразование датума возможно выполнить, если к геоцентрическому преобразованию добавить четыре дополнительных параметра. Семь параметров - это три линейных сдвига (DX,DY,DZ), три угловых поворота вокруг каждой оси (r x ,r ,r ), и коэффициент(ы) масштаба.

J LZ J original

Значения поворота даются в десятичных секундах, в то время как коэффициент масштаба выражается в частях на миллион (parts per million - ppm). Поворот можно определить двумя различными способами. Угол поворота может иметь положительные значения либо при повороте по направлению по часовой стрелке, либо по направлению против часовой стрелки, если смотреть на начало системы координат X,Y,Z.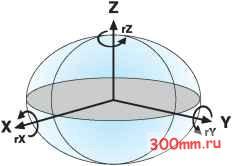

Определение углов поворота в системе координат (или определение Бурса-Вольфа).

Уравнение, приведенное в предыдущем столбце, показывает, как такие уравнения записываются в Соединенных Штатах и в Австралии, и носит название преобразования путем поворота системы координат. Значения поворота положительны при вращении против часовой стрелки. В Европе используется другое преобразование, называемое преобразованием радиуса-вектора. Оба метода иногда называют методом Бурса-Вольфа. В Projection Engine метод преобразования систем координат и метод Бурса-Вольфа - это одно и то же. Поддерживаются и метод преобразования систем координат, и метод радиуса-вектора, и достаточно просто конвертировать значения преобразований из одного метода в другой путем простого изменения знаков трех значений углов поворота. Например, для перехода от датума WGS 1972 к датуму WGS 1984 методом преобразования системы координат необходимы следующие параметры (в следующем порядке, DX,DY,DZ,r x ,r у ,r z ,s):

(0.0, 0.0, 4.5, 0.0, 0.0, -0.554, 0.227)

Для того, чтобы использовать те же самые параметры для преобразования по методу радиуса-вектора, измените знак угла поворота. Новые параметры выглядят так:

(0.0, 0.0, 4.5, 0.0, 0.0, +0.554, 0.227)