мин ; о - частота вращения вала двигателя, мин ; Рд - мощность на валу двигателя, кВт.

Ддя определения вращающего момента по мощности и частоте вращения можно пользоваться и номограммой (рис. 7).

50 40

0,-1

0,6 0.5

0,4 0.3

7=974, если Р в кВт

8000 6000

чооо

у 2 ООО

800 600

399 - 200

0 30 20

0,8 0,6

со со

Схема пользования

20 4

50- 60

§

%. 100 со

&

§

SO О 600

890 Л WOO

Рис. 7. Номограмма ддя определения вращающего момента (кН см) по

мощности и частоте вращения

Определение нагрузок на валы

За расчетную нагрузку принимают максимальную длительно действующую нагрузку.

Расчетную нагрузку определяют:

по мощности (задаваемой обычно на

входе и выходе коробки передач), КПД и

скорости;

по моментам или силам (задаваемым обычно тоже на входе или выходе), передаточному отношению и КПД.

Расчетную частоту вращения вала, мин, выбирают соответственно по частоте вращения шпинделя пл или выходного вала коробки, при которой они передают наибольшие моменты (обычно берут минимальную частоту вращения шпинделя, при которой передается полная мощность).

Окружная сила на зубчатых колесах и цепных звездочках

где d - делительный диаметр зубчатого колеса или цепной звездочки; Т - вращающий момент.

Нагрузку на вал от цепной передачи приближенно принимают направленной параллельно ведущей ветви цепи и равной окружной силе, умноженной на коэффициент, зависящий от положения передачи (для горизонтальной передачи 1,15, для вертикальной 1,05).

Нагрузку на вал (в Н) от ременной передачи при расчете на усталость приближенно принимают направленной вдоль линии центров шкивов и определяют по формуле

e = 200ao/ sin,

Ведущая

R0,5P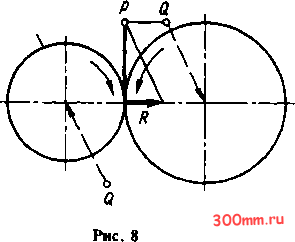

Й0,5Р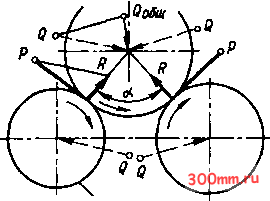

Ведущая

Рис. 9

где ао - начальное натяжение, обычно

принимаемое для плоскоременных передач равным 1,8 МПа, а для клиноременных 1,2-1,5 МПа; F - площадь поперечного сечения ремня, см; а - угол обхвата шкива, град.

Так как начальное натяжение при перетяжке в 1,5 раза больше нормального, то наибольшую нагрузку на вал можно определить по формуле

бтах =le = 300ao/sin.

На рис. 8-11 изображено графическое о пределе н ие с ил, действующих на вал и подшипники, по заданной окружной силе (для зубчатой передачи с углом зацепления а = 20°и с учетом угла трения р ~ 5 6°).

Ведущая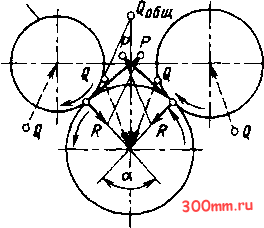

R=0,5P

Рис. 10

Ведущая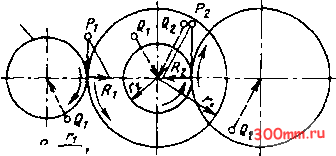

Рис. 11

Если нагрузки, действующие на вал, не лежат в одной плоскости, то их раскладывают по двум взаимно перпендикулярным координатным плоскостям и в каждой из этих плоскостей определяют реакции опор и изгибающие моменты, а затем проводят геометрическое суммирование.

Нередко расчет может быть упрощен удачным выбором координатных плоскостей. Например, если окружные силы от ведомого и ведущего элементов взаимно параллельны или взаимно перпендикулярны, то оси координат следует направлять вдоль действия этих сил. Отклонениями от параллельности или перпендикулярности в пределах 10-15° следует пренебрегать, совмещая силы с осями координат. Допускается также совмещение сил в одну плоскость, если угол между ними не более 30°.

Определение реакций опор и изгибающих моментов

При расчете вал принимают за балку, лежащую на щарнирных опорах. Эта расчетная схема точно соответствует действи-

тельному положению только для валов на подшипниках качения, установленных по одному или по два в опоре; при двух подшипниках должна быть обеспечена самоус-танавливаемость опоры; например, установкой конических роликоподшипников вершинами роликов в разные стороны.

Для других опор такую расчетную схему можно применять как приближенную. При длинных несамоустанавливающихся подшипниках скольжения, расположенных по концам вала, равнодействующую реакции подшипника следует предполагать приложенной к точке, отстоящей от его кромки со стороны пролета на 1/3-1/4 длины подшипника.

При расчете валов, вращающихся в длинных подшипниках скольжения (l/d = 3), расчетная схема приближается к схеме балки с заделанными концами.

В табл. 8 и на рис. 12 приведены формулы для определения реакций опор и изгибающих моментов двухопорных валов с характерными случаями нагружения.

8. Определение реакций а опорах

А, А

1. = 1 + 2 + Ъ.

В - В\ + Bj + By (алгебраическая сумма).

2. Если приложенная сила Qn имеет направление, обратное указанному на рисунке, то реакции в опоре An и Вп меняют знак на обратный.

3. Qn = А + Вп (для проверки).