хОу, то линия, на которой лежит вектор Ге, пересекает координатную плоскость хОу в некоторой точке Мг-

Из курса аналитической геометрии известно, что угол, образованный плоскостью, перпендикулярной прямой, на которой лежит вектор v, и прямолинейной главной режущей кромкой, по определению равный кинематическому углу наклона \, подчиняется следующей зависимости:

(5.6)

sin Х, = cos tti cos 0L2 + cos Pi cos P2 -I--I- COS Yi cos Y2,

где costti, cosPi, cosYi - направляющие косинусы прямой, на которой лежит вектор Ve, cos 2, C0SP2, C0SY2 - направляющие косинусы прямолинейной главной режущей кромки.

Чтобы значения направляющих косинусов COS tti, cos Pi, cos Yi для прямой, на которой лежит вектор г, выразить через функции углов г и е, рассмотрим схему на рис. 5.11. Отрезок М2М3, параллельный оси X, образует с отрезком М1М2 угол ai; отрезок М2М4, параллельный оси у, образует с отрезком М1М2 угол Pi; отрезок М1М5, параллельный оси z, образует с отрезком М1М2 угол Yi- Отрезки М1М2 и МlAfs лежат в плоскости, касательной к цилиндрической поверхности траектории. Поэтому отрезки М1М3 и MiMs расположены под углом е, а отре:ки М1М2 и М1М3 - под углом г. Из системы треугольников следует: cos tti = sin г; -J

COSPi = M2M4/M1M2; >

cosy =MiMi/MiM2, J

гдеМ2М4 = MiMs = MiM3sine;MiM2 = = MiM3/cosr; M1M5 = MiM3Cose, откуда направляющие косинусы

(5.7)

costti = sin r; J cos Pi = cos г sin e; > cos Yi = cos г cos e. J

Чтобы найти значения направляющих косинусов cos а.2, cos Р2, cos Y2 для прямолинейной главной режущей кромки и выразить их через известные углы ф и X,

рассмотрим схему на рис. 5.12. Здесь отрезок М1М3 параллелен оси х и образует с главной режущей кромкой М1М2 угол а.2. Отрезок МуМ параллелен оси у и образует с главной режущей кромкой угол Р2- Угол наклона X заключен между отрезками MiMs и М1М2, а угол в плане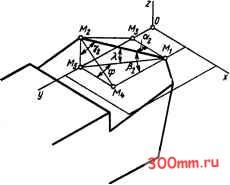

Рис. 5.12. Схема определения направляющих косинусов прямолинвйной режущей кромки

Ф - между отрезками М1М5 и М4М5. Из системы треугольников получаем:

cosa2 = М1М3/М1М2; 1

cos Р2 = М1М4/М1М2; >

cos Y2 = sin X, J

где MiM3 = MMs = MiMs cos ф; M1M2 = MiMj/cosX; M1M4 = = M1M5 sin Ф, откуда

(5.8)

cos a2 = cos Ф cos X; )

cos P2 = sin Ф cos X; >

cos Y2 = sin X. J

Подставив значения направляющих косинусов, определенных по формулам (5.7) и (5.8), в уравнение (5.6), получаем уравнение для кинематического угла наклона главной режупдей кромки резца:

(5.9)

sin Хк = cos ф cos X sin г -I-

-I- sin ф cos X sin е cos т) -I- sin X cos г cos e.

Можно отметить, что в общем случае различные точки главной режущей кромки расположены на разных расстояниях от

оси вращения заготовки, и угол е и угол подъема г) траектории результирующего движения резания переменны по длине режущей кромки. Поэтому значение кинематического угла наклона X, также является величиной переменной на всем протяжении главного режущего лезвия. Если

где cos o-t, COS Pi, cos 71 - направляющие косинусы вектора Ъ определяемые по уравнениям (5.7).

Уравнение линии сбега стружки по передней поверхности резца имеет вид (5.11)

(х - xo)/cos 3 = (у - yo)/cos Рз = = (z-zo)/cos73.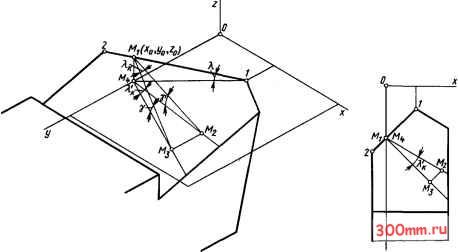

Рис. 5.13. Схема определения угла сбега стружки

угол X = О и главная режущая кромка лежит на высоте оси О вращения заготовки, то угол е = О и уравнение (5.9) принимает вид

sin X, = cos ф sin Г).

sm 7к

где cos 3, cos Рз, cos 73 - направляющие косинусы линии сбега стружки, лежащей на передней поверхности резца.

Искомый угол 7к согласно его определению и положениям аналитической гео- метрии находят по уравнению

cos tti COS 3 + COS Pi cos Рз + COS 7i cos 73

/cos OLi + cos Pi + cos 7i /cos 3 + COS Рз -I- COS 7з

КИНЕМАТИЧЕСКИЙ ПЕРЕДНИЙ УГОЛ. По определению кинематический передний угол 7 измеряется между плоскостью, перпендикулярной вектору скорости результирующего движения резания, и линией сбега стружки по передней поверхности. Используя математический аппарат аналитической геометрии, запищем уравнение плоскости, перпендикулярной вектору Ve в некоторой точке Ml (рис. 5.13) главного режущего лезвия, имеющей координаты (хо, Уо. о): (5.10)

(х - Хо) cos tti + (у - уо) cos Pi + + {z - Zo)cos7i = О,

Теперь выразим значения направляющих косинусов со8аз, C0SP3 и COS73 линии, в направлении которой по передней поверхности резца сбегает срезаемая стружка, через значения угловых параметров резца. На рис. 5.13 линия сбега стружки, обозначенная отрезком MiM, и отрезок М1М3 линии пересечения передней поверхности с главной секущей плоскостью лежат в плоскости передней поверхности резца и пересекаются между собой под углом Х. Отрезки М2М4 и М3М4 лежат в горизонтальной плоскости хОу и являются проекциями на нее соответ-

ственно отрезков MiMj и М1М3. Отрезки М1М3 и М3М4 лежат в главной секущей плоскости и пересекаются между собой под углом, равным переднему углу у. Отрезки М1М2 и М2М4 пересекаются под углом у, который определяется следующим образом: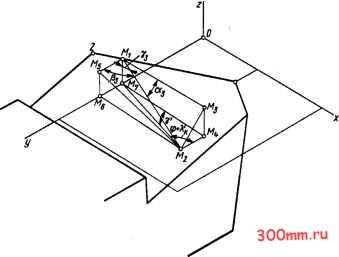

соваз = М1М3/М1М2; 1

cos Уз = sin у = sin у cos Х. J

где М1М3 - ММ- = М2М7 sin(9 -1- Хк); М1М2 = М2Мт/со$ук =

= M2M7/l/r-sin7cosX; MiM, = = М2М4 = М2М7со5(ф + ху, откуда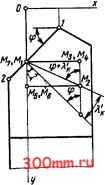

Рис. 5.14, Схема определения направляющих косинусов лини 1 сбега стружки

sin у = М1М4/М1М2,

примем М1М4 = MiM3siny; MjMj = = M1M3/COS Х откуда

siny= sinycosK; i

[ (5.13)

cos у = /l - sin у cos Xk-J

Из рис. 5.13 также следует, что угол Х, лежащий в плоскости хО>, рассчитывается по уравнению

(5.15)

cos осз = sin (ф ч- ху /l - sin у cos Х; cos Рз = cos (ф + Xi) \/l - sin у cos X; cos Уз = sin у cos Xk.

Подставляя значения направляющих косинусов из уравнений (5.7) и (5.15) в уравнение (5.12), получаем уравнение для определения кинематического переднего угла:

(5.16)

sin у = l/l - sin у cos Хк [sin (ф + Ху sin г) + -I- cos (ф -1- ху cos Г) sin е] -t- sin у cos X cos ri cos к.

(5.14)

tg X; = tg X/cos y.

Направляющие косинусы для линии MjMj сбега стружки по передней поверхности находят по схеме на рис. 5.14 из системы прямоугольных треугольников:

Уравнение (5.16) показывает, что кинематический передний угол у является переменной величиной по длине главной режущей кромки и его значение зависит от исходной геометрии резца, полученной при заточке, от соотнощения режимных параметров - подачи S и скорости резания V, косвенно выраженных углом г], а также от диаметра обрабатываемой за-