готовки, выражаемого углом е. В частном случае, для резца с углом X = О, вершина которого находится на высоте оси вращения заготовки (е = О), уравнение (S.16) принимает вид

sin Yk = cos Y sin ф sin Г) + sin у cos Г.

(5.18)

dx/dco = 5/(2я); dy/d(o = (-D sin co)/2; dz/dto = (D cos co)/2. Используем зависимости (5.18) для выве-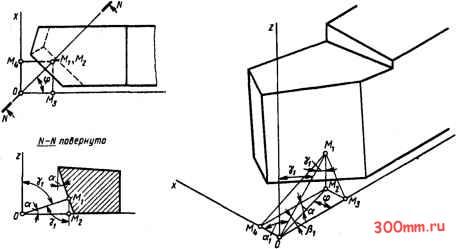

Рис. 5.15. Схема определения направляющих космнусов перпендикуляра, опущенного но главную зоднюю поверхность

КИНЕМАТИЧЕСКИЙ ЗАДНИЙ УГОЛ, fjo Определению, кинематический задний угол а,! заключен между линиями, одна из которых является касательной к винтовой траектории результирующего движения точки М (см. рис. 5.10), на которой лежит вектор й а другая - касательной к линии MMi пересечения задней поверхности резца цилиндром диаметром D, на котором лежит винтовая траектория. Винтовая траектория описывается параметрическими уравнениями следующего вида:

(5.17)

X = 5со/(2я);

y = (Z)cosco)/2;

Z = (D sin со)/2,

где ю - угловая координата точки M , лежащей на винтовой траектории. Взяв первые производные от уравнений (5.17), получим:

дения уравнения касательной к винтовой траектории:

(5.19)

2я(х - Хо) -2(у - Уо) 2(2 - zo)

£>sin (О

Dcosco

На рис. 5.15 приведена схема для вывода уравнения плоской главной задней поверхности или плоскости, касательной в точке Ml к криволинейной главной задней поверхности. Направляющие косинусы перпендикуляра OMi, опущенного на плоскость главной задней поверхности из начала координат, находятся из системы прямоугольных треугольников:

cos tti = ОМ4/ОМ1; cos Pi = OM3/OM1; cos Yi = sin a,

где OM4 = M2M3 = ОМ 2 sin ф; OMi = = OM2/cos a; OM3 *= OM2 cos Ф, откуда

(5.20)

costti = COS a sin ф; cos Pi = cos a cos ф; cos Yi = sin a.

Уравнение плоской задней поверхности или касательной плоскости, приведенной к криволинейной задней поверхности через некоторую точку М главной режущей кромки (см. рис. 5.10), имеет йид (5.21)

(х - Хо) cos а sin ф + (у - уо) cos а cos ф + + (z - zo) sin а = О,

(5.25)

(x-xo)sinф

и (COS ф sin со - tg а cos со)

У-Уо

Z - Zo

D sin со D cos со

Для точек главной режущей кромки, лежащих на высоте оси вращения заготовки, угловой параметр со = 0. Для точек, лежащих выще или ниже оси заготовки на размер ±Н, угол со = е = = arcsin {2H/D).

Учитывая это, кинематический задний угол о связан с исходной геометрией резца и его расположением относитель-

где Хо, Уо, Zo - координаты точки М. ° и вращения заготовки, а также с Используя параметрические уравнения Диаметром D заготовки следующей за-

поверхности, на которой лежит винтовая траектория,

(5.22)

х = р;

у = (£)cosco)/2; Z = (£) sin со)/2

висимостью: (5.26)

cos ак =

£) sin ф + D (cos ф sin е - tg а cos е)/(2п) l/sin ф + (cos ф sin е - tg а cos е) \/п + [£)/(2п)]

и уравнение (5.21), совместным их реще- Для резца с углом Х = 0, установленного нием находим уравнение линии ММ г так, что его верщина находится на вы-пересечения главной задней поверх- соте оси вращения заготовки, кинемати-ности резца с цилиндром диаметром D:

(5.23)

, Г/ Dcosco\ / £)sinco\ 1, .

= Хо+ уо--2-)° ф - zo + -2-

y = (£)cos со)/2; Z = (£) sin со)/2.

Взяв первые производные от уравнений ческий задний угол о может быть найден

/ ОЧЧ ттг,1,ИМ - тт .- .....

(5.23), получим: (5.24)

. ,. D cos ф sin со - £) tg а cos со

dx/dco =----------

2 sin ф

dy/dco = {-Dsm со)/2; dz/dco = (D cos co)/2.

Теперь можно записать уравнение касательной в точке М к линии MMi пересечения задней поверхности резца цилиндром радиуса диаметром D:

с помощью следующего выражения:

cosa.

P[sinф-tga/(2л)]

l/sin ф -I- tg aj/D -I- 1П/(2к)У

процесс образования стружки

§ 6.1. ЭКСПЕРИМЕНТАЛЬНЫЕ ИССЛЕДОВАНИЯ ПРОЦЕССА РЕЗАНИЯ

Характерная особенность процесса резания состоит, во-первых, в том, что лезвия режущего инструмента срезают припуск слоями, толщина поперечного сечения которых обычно меньше 1 мм (лишь на тяжелых станках толишна срезаемого слоя доходит до 2 мм); во-вторых, физико-механические свойства поверхностных слоев, которые подвергаются пластическому деформированию и превращению в стружку, отличаются от свойств материала в глубине заготовки; в-третьих, в результате деформирования и разрушения материала срезаемого слоя происходит возникновение из монолитной массы двух новых поверхностей - одной на обрабатываемой заготовке, а другой - на срезанной стружке.

Еще в конце прошлого века при первых систематических исследованиях процессов реза1шя металлов было установлено различие в образовании и внешнем виде стружек, срезанных с заготовок из различных материалов, а также зависимость внешнего вида стружки от скорости резания и толщины срезаемого слоя. Выяснилось, что характер деформации и разрушения в объеме срезаемого слоя металла подчиняется определенным закономерностям и зависит от вида металла и баланса действующей системы механических сил, возникающих в процессе резания.

Первые капитальные научные исследования закономерностей деформации металла в процессе резания и классификация стружек по их внешнему виду были выполнены в конце прошлого и в начале этого веков основоположниками теории резания металлов, русскими учеными И. А. Тиме, А. А. Бриксом, К. А. Зворы-

киным, Я. Г. Усачевым. Большой вклад в исследования пластической деформации в процессе стружкообразования внесли советские ученые И. М. Беспрозванный,

A. В. Панкин, А. И. Каширин, В. Д. Кузнецов, С. Ф. Глебов, А. М. Розенберг,

B. А. Кривоухов, М. И. Клушин, Н. И. Зо-рев, А. И. Исаев, В. Ф. Бобров, М. Н. Ларин, П. П. Грудов и др. Разработанные русскими и советскими учеными теоретические положения, подтвержденные обширными экспериментальными исследованиями, составляют основу современных представлений о физических процессах, происходящих при стружкообразовании и возникновении новых поверхностей на обрабатываемых деталях.

ИССЛЕДОВАНИЯ ПРОЦЕССА СТРУЖКООБРАЗОВАНИЯ И. А. ТИМЕ. Первые исследования закономерностей деформирования металла в процессе стружкообразования были проведены профессором Санкт-Петербургского политехнического института И. А. Тиме и их результаты опубликованы в 1893 г. В качестве объекта исследования был взят свинцовый брусок прямоугольного сечения. Для облегчения наблюдений на гладко отполированной боковой стороне бруска через равные интервалы длиной / были нанесены керном метки (рис. 6.1). На строгальном станке с верхней грани бруска по всей ее ширине резцом, прямолинейное лезвие которого имело главный угол в плане ф = 90° и угол наклона лезвия >. = О, срезался слой толщиной а. Резание производилось с малой скоростью. На рис. 6.1, - д1 схематически показан ряд последовательных положений, занимаемых резцом на пути его рабочего движения. Преодолевая сопротивление металла на пути своего перемещения, лезвие резца пластически деформирует и сдвигает металл в сторону от передней поверхности (рис. 6.1, б). О пределах распространения пластической деформации в срезаемом слое И. А. Тиме судил по потускнению полированной боковой стороны свинцового бруска. Визуальными наблюдениями было установлено, что распространение пластической деформации впереди движущегося лезвия резца ограничено движущейся синхронно с лезвием линией, образующей угол О с направлением движения