гласно правилам сложения векторов значение равнодействующей силы резания

P, = ]/Pl + Pl + Pl

§ 7.2. ТЕОРЕТИЧЕСКОЕ

УРАВНЕНИЕ

СИЛЫ РЕЗАНИЯ

ВЫВОД УРАВНЕНИЯ СИЛЫ РЕЗАНИЯ. Один из основоположников теории резания металлов, русский ученый К. А. Зворыкин, исходя из положения, что сила резания Р (составляющая Р) равна сопротивлению металла обрабатываемой заготовки пластической деформации стружкообразования и силе трения на поверхностях лезвия резца, вывел теоретическое уравнение силы резания. В основу вывода им были положены расчетные схемы, отражающие работу строгального резца, перемещающегося относительно заготовки со скоростью i;.

На рис. 7.4 показана система сил, приложенных в процессе резания к передней и задней поверхностям лезвия строгального резца со стороны материала обрабатываемой заготовки. В точке М к передней поверхности лезвия резца приложены приведенная нормальная сила Q, перпендикулярная передней поверхности резца, и приведенная сила трения fiQ, возникающая в связи с перемещением стружки по передней поверхности (/i - коэффициент внешнего трения скольжения обрабатываемого и инструментального материалов). В точке О к задней поверхности лезвия резца приложены приведенная сила R, перпендикулярная направлению главного движения резца со скоростью i;, и приведенная сила трения fiR, направленная против направления движения резца. Сила резания Р приложена в точке М к передней поверхности; по направлению действия она совпадает со скоростью i; перемещения строгального резца.

Из условия равновесия следует, что сила Р равна сумме проекций всех сил, приложенных к лезвию резца, на прямую А-А, вдоль которой действует сила Р. Проецируя рассмотренные силы на гори-

зонтальную линию А-А, получаем уравнение (7.1)

Р = Q cos у -I- /iQ sin у -I- fiR.

Используя принцип равновесия системы и проецируя рассмотренные выше силы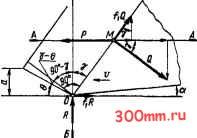

Рис. 7.4. Схема сбалансированных сил, действующих на лезвие резца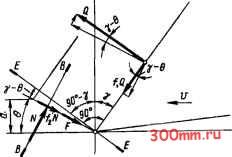

Рис. 7.5. Схема сбалансированных сил сопротивления металла пластической деформации и разрушениям при стружкообразовании

на вертикальную линию Б-Б, имеем (7.2)

R = Q sin у - fiQ cos у.

Подставив полученное по уравнению (7.2) значение силы R в уравнение (7.1), получаем

Р = Q cos у -t-/iQ sin у -I-+ /i6siny-/iecosy, или (7.3)

P=e[(l-/f)cosy--2/isiny].

в уравнении (7.3) сила Q определяет сопротивление металла пластической деформации стружкообразования. В рассмотренной схеме стружкообразования пластическая деформация условно протекает только в плоскости скальшания. Рассматривая систему сил, действующую в зоне стружкообразования на пластически деформируемый металл, К. А. Зворыкин представил сопротивление пластической деформации тремя приведенными силами: а) нормальной силой N; б) силой внутреннего трения /2А?, где /2 - коэффициент внутреннего трения в пластически деформируемом металле; в) силой F, образованной касательными напряжениями, действующими в плоскости скалы-

слое пластически деформируемого металла возникают касательные напряжения т. Результирующая этих напряжений на рис. 7.5 представлена силой F = abx/sin 6, где а - толщина срезаемого слоя; Ь - ширина срезаемого слоя. Проецируя действующую на металл в зоне стружкообразования систему сил на линию плоскости скалывания, из условий равновесия находим

F = Q cos (Y - в) -I- /iQ sin (у - 6) -

- fifiQ cos {у-е)+ hQ sin (Y - 6),

откуда сила Q, нормальная к передней поверхности резца, учитывая Выражение для силы F, равна

(7.5)

[(1 - /1/2) cos (y - в) -I- (/i -I- /2) sin (y - 6)] sin e

вания (рис. 7.5). Направление сосредоточенной нормальной силы N совпадает с линией В-В, перпендикулярной плоскости скалывания. Плоскость скалывания образует угол 6 с направлением главного движения строгального резца и угол (Y - в) с линией Е-Е, перпендикулярной

Подставив полученные значения силы Q в уравнение (7.3) и исходя из предпосылки о равенстве сил, одновременно действующих на лезвии резца и в плоскости скалывания, можно вывести теоретическое уравнение силы резания:

(7.6)

аЬт [(1 - f\) cos у + 2/i sin у]

sinG[(l -/i/2)cos(y - G) + (/, +/2)sin(y - в)Г

передней поверхности лезвия, заточенного под углом у.

На рис. 7.4 силы Q fiQ рассматривались приложенными к резцу. На рис. 7.5 те же силы рассматриваются приложенными к стружке, поэтому они действуют в противоположном направлении. Проецируя на линию В-В действующие в этой системе силы, из условий равновесия получаем (7.4)

N =/iGcos(Y - G) - Gsin(Y - G).

Тогда сила внутреннего трения металла в плоскости скалывания равна

fiN = /1/2G cos (у - 6) - /2G sin (у - G).

К. А. Зворыкин принял, что в плоскости скалывания по всей ее площади в тонком

РАЗВИТИЕ ТЕОРЕТИЧЕСКИХ ИССЛЕДОВАНИЙ УРАВНЕНИЯ СИЛЫ РЕЗАНИЯ. После того как К. А. Зворыкиным было выведено уравнение теоретической силы резания в вышеприведенном виде, на основе той же предпосылки о равенстве сил, действующих на резец, и сопротивления металла пластической деформации стружкообразования был предложен ряд аналогичных уравнений. Их авторы отразили в них несколько иные представления о системе действующих приведенных сил, специфике пластической деформации стружкообразования, а также о геометрической форме зоны максимальных пластических деформаций, заменяющей понятие о плоскости скалывания. Вывод этих уравнений и их анализ подробно изложены в трудах советских

ученых А. М. Розенберга, И. М. Клушина, Н. Н. Зорева, В. Ф. Боброва, М. Ф. По-летика, В. А. Кривоухова и др.

УПРОЩЕННОЕ УРАВНЕНИЕ СИЛЫ РЕЗАНИЯ. Для решения некоторых производственных задач иногда требуется ориентировочно определить уровень возможных сил резания при механической обработке. Для зтого желательно иметь достаточно простую математическую зависимость. Принимая во внимание уравнение (3.3), уравнение (7.6) можно записать в виде (7.7)

Р = ет/ , где

и, следовательно, сила резания Рк 2,5 0,61 1,5 2,3 кН. Если предел прочности стали неизвестен, но известна или может быть оперативно определена его твердость по Бринеллю, то с достаточной степенью точности предел прочности можно определить по уравнению ств 0,31 НВ.

§ 7.3. ИЗМЕРЕНИЕ СОСТАВЛЯЮЩИХ СИЛЫ РЕЗАНИЯ ДИНАМОМЕТРАМИ

Как правило, в теоретически выведенные уравнения входят параметры, чис-

(1-/0 cosY-b2/iSinY

sin е [(1 - /1/2) cos (y - 9) -Ь (Л + h) sin (y - 9)]

- коэффициент, учитывающий влияние всех безразмерных величин ;/ = аЬ - площадь поперечного сечения срезаемого слоя. Произведение ех можно заменить эквивалентным произведением Л!рСТв, где сТв - предел прочности обрабатываемого металла на растяжение. Подставив это выражение в уравнение (7.7), получаем упрощенное уравнение силы резания (7.8)

Р = КрСТв/ .

в уравнении (7.8) произведение КрСТд выражает удельное сопротивление резанию металла обрабатываемой заготовки и его принято называть коэффициентом резания. Экспериментально установлено, что при резании углеродистых конструкционных сталей Кр 2,5. Для других марок конструкционных сталей в зависимости от их химического состава, структурного состояния и механических свойств коэффициент Кр = 2,3... 2,8. Упрощенное уравнение (7.8) силы резания позволяет в первом приближении оценить значение силы, действующей в процессе резания. Например, при резании углеродистой стали 45 с глубиной резания t = 3 мм и подачей S = 0,5 мм/об площадь поперечного сечения срезаемого слоя / = 1,5 мм . Предел прочности стали 45 сТв = 0,61 ГПа (см. табл. 1.1)

ловые значения которых неизвестны и зависят от режимов резания и степени износа лезвий резца. Найти значения этих параметров можно лишь экспериментально, выполнив непосредственные измерения силы резания Р специальным динамометром. Поэтому все теоретически выведенные уравнения предназначены лишь для качественного анализа зависимости силы резания Р от режимных, геометрических и физических параметров и не используются на практике как рабочий математический аппарат для количественного выражения действующих сил резания.

Нормирование режимов резания для условий производства ведут по уравнениям, математически описывающим результаты определения составляющих Р,., Ру и Рг силы резания специальными динамометрами.

НАЗНАЧЕНИЕ И ПРИНЦИП РАБОТЫ ДИНАМОМЕТРОВ. Принцип действия всех динамометров основан на измерении упругой деформации измерительных элементов динамометров, пропорциональной значению измеряемой составляющей силы резания. Динамометры, имеющие лишь один измерительный элемент, используемый обычно для измерения вертикальной (главной) составляющей Рг силы резания, называются о д н о-