
 |
|
Читаемые статьи
Читаемые книги
Ссылки
|
Главная > Технологические способы металлообработки компонентными. Динамометры, имеющие два взаимно перпендикулярно расположенных измерительных элемента, например, для одновременного измерения вертикальной и горизонтальной Р, составляющих, называются двух-компонентными. Динамометры, 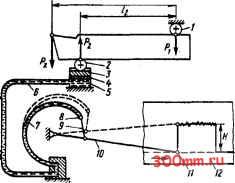 Рис. 7.6. Схема ианерения силы резания гидравлическим динанометрон имеющие три взаимно перпендикулярно расположенных измерительных элемента для одновременного измерения всех трех составляющих Р Ру и Р, называются трехкомпонентными. Измерение упругих деформаций измерительных элементов токарных динамометров может осуществляться принципиально различными способами, из которых наибольщее распространение получили гидравлический и тензометрический. ГИДРАВЛИЧЕСКИЕ ДИНАМОМЕТРЫ. Принципиальная схема гидравлического измерительного устройства показана на рис. 7.6. На лезвие резца действует вертикальная составляющая Р силы резания. Нижней опорной плоскостью резец через щарик 2 опирается на порщень 3. Задним концом державка резца через щарик / опирается на неподвижную опору корпуса динамометра. Сила Рг, действующая на порщень, боль-ще измеряемой составляющей Р в Zj/Zj раз, т. е. Рг = PJilh- Порщень 3 с силой Рг давит через гибкую прокладку 4 на жидкость, заполняющую емкость 5. Давление в жидкости р = РгМ, где А - площадь поршня 5, и передается через отводную трубку 6 на изогнутую трубчатую пружину 7. Под действием давления упруго деформируемая пружина разгибается и через рычаг 9, соединенный с ней шарниром 8, перемещает вверх стрелку 10 с пером 11. Перо, отклоняясь, оставляет на движущейся слева направо бумажной ленте 12 запись. Отклонение Н пера в любой точке записи пропорционально 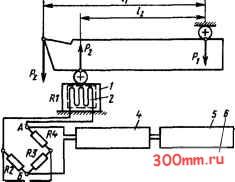 Рис. 7.7. Схема измерения силы резания тен-зоэлектрическим динамометром силе Pj. По отклонению пера, измеряемому в единицах длины (мм), с помощью тарировочного графика или таблицы находят значение составляющей силы Рг = Pihlh в единицах силы (кН). На ленте регистрирующего устройства трехкомпонентного гидравлического динамометра стрелки трех автономно действующих измерительных устройств производят записи для составляющих Р Ру и Р, измеряемой силы резания. ЭЛЙKTPИЧECKИE ТЕНЗОМЕТРИ-ЧЕСКИЕ ДИНАМОМЕТРЫ. Принципиальная схема электрического измерительного устройства показана на рис. 7.7. Здесь базирование резца и силы Р Pi и Рг, действующие на него, такие же, как для гидравлического динамометра, и, следовательно, на упругий измерительный элемент 1 оказывает воздействие сила Р2 = Pzhlh- На упругий элемент 1 наклеен тензометрический датчик 2. При наклейке датчика на упругий элемент его ориентируют таким образом, чтобы направление участков проволоки с большей протяженностью (база датчика) совпадало с направлением ожидаемых упругих деформа- ций. Для измерения сопротивления датчика используется мостовая схема из сопротивлений R1, R2, R3 и R4, в которую датчик сопротивлением R1 подсоединяется в качестве одного из плеч моста. Упругая деформахщя измерительного элемента 1 и, следовательно, наклеенного на нем датчика приводит к изменению сопротивления R1 датчика и нарушению баланса моста, питаемого напряжением от источника 3. Возникает разность потенциалов между точками А и Б моста, значение которой пропорционально изменению сопротивления R1 датчика, соответствующему деформации упругого элемента под действием силы Рг- Подсоединенный к точкам А и Б моста усилитель 4 усиливает сигнал разбаланса, который затем поступает на регистрирующий прибор 5. Отклонение Н на ленте 6, зафиксированное при резании, может быть пересчитано в значение действующей при резании составляющей силы резания Р согласно предварительно проведенной тарировке. Токарные динамометры за счет конструктивного исполнения с использованием описанной схемы замера одной составляющей силы резания обеспечивают одновременную запись всех трех составляющих Р Ру и Р. § 7.4. аппроксимация результатов динамометрического измерения составляющих силы резания АППРОКСИМАЦИЯ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ. Рассмотрим методику графоаналитической обработки динамометрических измерений силы резания Р при переменных значениях некоторого независимого режимного параметра X. Произвольно взятые значения Xi, Х2, х независимого режимного параметра и соответствующие им измеренные динамометром значения силы резания Р Рг, Р после проведения измерений записывают в форме протокола:
Используя протокольные записи как значения координат, на графике (рис. 7.8) наносят полученные экспериментальные 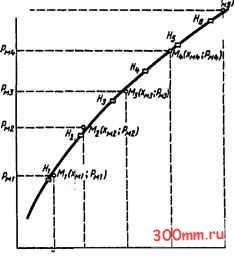 Рис. 7.8. Графическое ыражение линейных координатах рмультатов юмерения силы ремния точки Ml, Ml, М . Через экспериментальные точки проводят плавную выравнивающую линию, графически приближенно выражающую искомую функциональную зависимость Р = / (х). Если эта кривая по своему виду схожа с параболой, то искомую функциональную зависимость Р = / (х) можно попытаться аппроксимировать функцией степенного вида (7.9) Р = сх , где коэффициент с и показатель степени и являются константами. Чтобы найти значения констант сим, удобно провести логарифмирование выражения (7.9). Тогда получаем выражение (7.10) lgP = lgC + MlgX. На графике в двойных логарифмических координатах вырание (7.10) имеет вид прямой (рис. 7.9). (При этом на шкалах двойных логарифмических координат от-кладьтают истинные значения параметров Р и X.) Числовые значения показателя степени и и коэффициента с в уравнении (7.9) могут быть найдены графическим и аналитическим способами. При графическом способе на рис. 7.9 строят прямоугольный треугольник с катетами А п Б, гипотенузой которого может быть произвольный отрезок выравнивающей прямой. Измерив длины катетов Аи Б с помощью линейки, значение показателя степени находят из выражения (7.11) U = tg т = А/Б. Значение коэффициента с определяют из условия с 1 = Р. Следовательно, чтобы найти значение с, на графике рис. 7.9 при значении х = 1 проводится вертикальная линия до пересечения с выравнивающей прямой. Значение Рд, соответствующее точке пересечения, численно равно искомому значению с. Значения показателя степени и и коэффициента с в степенной функции (7.9) могут быть найдены аналитическим способом без построения графика в двойных логарифмических координатах. Для этого на выравнивающей кривой, построенной в линейном масштабе (рис. 7.8), берется ряд произвольных точек Hi{xm; Рт), Н2(хт, Риг), Щ(хиъ; Рт), ... Н {х ; Р ). Для достижения точности, необходимой в инженерных расчетах, достаточно при аппроксимации взять на выравнивающей кривой пять - семь точек. Для этой же цели могут быть взяты и непосредственно экспериментальные точки, если они не имеют существенных отклонений от выравнивающей кривой и число их не превышает десяти. С увеличением количества взятых точек достоверность полученной расчетом аналитической функциональной зависимости растет, но еще в большей степени увеличивается объем производимых расчетных работ. Подстановкой в уравнение (7.10) координат взятых точек получаем ряд уравнений с двумя неизвестными и и с: IgP, =lgc-l-ulgxi; lgP2 = lgc + ulgX2; lgP3 = lgc-(- lgX3; lgPj = lgC-- lgXj. Объединяя попарно эти уравнения и решая системы из двух уравнений исключением коэффициента с, получаем несколь-Р 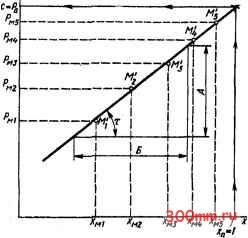 Рис. 7.9. Определение констант уравнения силы резания графическим и аналитическим способами ко выражений для параметра и: и = (Ig Pi - Ig p2)/(lg xi - Ig X2); = (lgPi-lgP3)/(lgXi-lgX3); u = (lgPi-lgPa/(lgXi-lgxa; U = (lgP2-lg/3)/(lgX2-lgX3): M = (Ig Pi 2 - Ig Pi)/(lg 2 - Ig Xi); M = (lgP, i-lgPO/(lgX, i-lgX.). Если значения показателя степени и, вычисленные по этим формулам, окажутся примерно одинаковыми, то это послужит доказательством, что искомая функциональная зависимость P = f{x) может быть удовлетворительно аппроксимирована степенным уравнением. Если же вычисленные значения и будут существенно различаться, например, больше, чем на 10%, это укажет на невозможность удовлетворительной аппроксимации результатов эксперимента степенным уравнением, и для решения поставленной задачи
|
 Чем хороши многотопливные котлы?  Нетрадиционное отопление  Детище отечественной Оборонки  Что такое автономное индивидуальное отопление?  Использование тепловых насосов  Эффективное теплоснабжение для больших помещений  Когда удобно применять теплые полы |
|||||||||||||||||||
|
© 1998 - 2025 www.300mm.ru.
При копировании материала обязательно наличие обратных ссылок. |