необходимо использовать уравнение другого вида. При удовлетворительной аппроксимации значение показателя степени и принимается равным либо среднему арифметическому всех вычисленных зна-

чений Мер.ар = Х *А2). либо среднему

квадратичному ир.в =

Зная значение показателя степени и, можно подсчитать числовые значения коэффициента с для всех точек, взятых на выравнивающей линии, с помощью уравнений вида С( = Pf/x , где i = 1, 2, ... . Окончательно значение коэффициента с определяется как среднее арифметическое

вычисленных значений с .

, = X cji, или 1

среднее квадратичное Сср.кв =

Определив графическим или аналитическим способом значения показателя степени и и коэффициента с, получим степенное уравнение Р = сх как конкретную форму выражения искомой функциональной зависимости Р = / (х). В функции (7.9) в роли параметра х могут выступать различные параметры, например ширина b или толщина а срезаемого слоя, твердость НВ обрабатываемого металла и др. Для каждого конкретного параметра показатель степени и и коэффициент с в формуле (7.9) имеют свои значения, которые вьмисляют по изложенной выше методике.

Аппроксимацию экспериментальных данных в общем случае можно производить с использованием функциональных зависимостей других видов, например линейной зависимостью у = а + Ьх, многочленами п-й степени и т. п. Однако в резании металлов преимущественное распространение нашли уравнения степенного вида как наиболее универсальные и позволяющие, выводя обобщенные уравнения степенного вида, учитывать в явном виде влияние на исследуемый параметр нескольких факторов.

ВЫВОД ОБЩЕГО ВИДА УРАВНЕНИЯ СИЛЫ РЕЗАНИЯ, в связи с тем что значение силы резания Р определяется комплексом различных параметров, главными из которых являются режимы резания и физико-механические свойства

обрабатываемого материала, экспериментальное нахождение искомой общей зависимости производится за несколько этапов.

На первом этапе обычно определяют частную функциональную зависимость Р = fi (t), где t - глубина резания. При этом экспериментальное измерение силы Р динамометром в целях исключения влияния побочных факторов (например, радиуса скругления вершины резца го) ведется с изменяющейся по значению шириной срезаемого слоя Ь. Такие условия возникают при точении трубы с переменной толщиной стенки. Остальные режимные и геометрические параметры резца на протяжении всего первого этапа экспериментов остаются постоянными. К числу таких параметров, требующих стабилизации, относятся: толщина срезаемого слоя, твердость металла обрабатываемой заготовки, скорость резания, наличие смазывающе-охлаждающей жидкости или ее отсутствие, главный и вспомогательный углы в плане, задний и передний углы, угол наклона главной режущей кромки. Вершина закрепленного в динамометре резца должна быть установлена строго на высоте оси вращения заготовки. Числовые значения силы резания Р, измеренные динамометром при различных значениях ширины b срезаемого слоя, заносятся в протокол.

При обработке большинства конструкционных сталей экспериментальные точки, нанесенные на график в линейных координатах, располагаются обычно так, что через них с достаточной степенью точности можно провести прямую линию, проходящую через начало координат. Следовательно, при аппроксимации экспериментальной зависимости уравнением вида

(7.12)

Р = cib

значение коэффициента Ci можно найти графическим способом по значению силы Р при fe = 1 мм, где Ci = Р.

Вьфазив в уравнении (7.12) ширину срезаемого слоя b через глубину резания t, по уравнению b = t/sin ф получим Р = = Cif/(sin ф) и, приравняв Сг = Ci/(sin ф) , находим, что искомая частная функциональная зависимость выражается степен-

ным уравнением (7.13)

Р = Cif.

На втором этапе выясняется частная функциональная зависимость Р = fiiS), где S - подача. Экспериментальное измерение силы Р динамометром на этом этапе обычно ведется с возрастающими по значению толщинами срезаемого еяоя а. Остальные режимные и геометрические параметры, включая щирину b фезаемого слоя, остаются постоянными. Значения силы резания, измеренные динамометром при различных толщинах а фезаемого слоя, заносятся в протокол. Как правило, экспериментальные точки, нанесенные на графике с линейными координатами, позволяют провести выравнивающую линию, имеющую форму параболы; это подтверждается тем, что на графике с двойньп1и логарифмическими координатами выравнивающая линия имеет форму прямой. На этом основании искомую функциональную зависимость можно выразить степенным уравнением

(7.14)

Р = сза .

Заменив в уравнении (7.14) толщину срезаемого слоя а подачей S согласно зависимости а = S sin ф, получаем Р = = сз (sin (pfS. Приняв С4 = Сз (sin tpf, окончательно получим (7.15) Р = с.

На третьем этапе при определении частной функциональной зависимости Р = /з (НВ) экспериментальное измерение силы резания динамометром ведется при резании металлов разной твердости НВ. Все остальные режимные и геометрические параметры остаются постоянными. Повторяя по вышеизложенной методике графическую и аналитическую обработку протокольных данных в том же порядке, как на первом и втором этапах, находим искомую зависимость, выражаемую степенным уравнением Р = Cs {HBf. Для практического использования это уравнение можно упростить, если условно принять НВ = 200. Тогда отношение действительной твердости по Бринеллю (НВ)

к условно принятой будет безразмерной величиной НВ/200 0,5... 2, т. е. мало отличающейся от единицы. Заменив выражение твердости НВ через отношение НВ/200, находим, что зависимость Р = = /s (НВ/200) имеет следующий вид: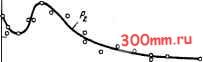

1*0 80 т iso

1 Цм/мии

Рис. 7.10. Зависимость составляющих силы резания от скорости реюния

(7.16)

Р = Сб (НВ/200),

где Сб = С52ОО .

На четвертии этапе определяют частную функциональную зависимость Р = = /4 (f), где v - скорость резания. В некоторых литературных источниках при решении практических задач, связанных с обработкой металлов резанием, силу резания Р принято полагать не зависящей от скорости резания v. В действительности это не совсем так. Непосредственные измерения динамометрами показьшают, что все составляющие Р, Ру и Р силы резания с увеличением скорости резания v, например при обработке углеродистых конструкционных сталей, изменяются согласно зависимостям, одна из которых представлена на рис. 7.10, где обработка производилась твердосплавным резцом Т15К6 с подачей S = 0,3 мм/об и глубиной резания t = 4 мм. В рассматриваемом случае зависимости не являются, как раньше, монотонными, а имеют экстремальные точки. Они уже не могут быть выражены одним степенным уравнением

достаточно простого вида. Для получения приближенного, но удовлетворяющего по точности, а также удобного для применения на практике математического выражения целесообразно вновь перейти к построению в двойных логарифмических координатах выравнивающей линии. Экс-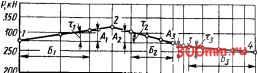

30 ио 50 60 70 80 90100 120 т Цм/мии

Рис. 7.11. Зависимость составляющей силы резания от скорости резания в двойных логарифмических координатах

периментальные точки в этом случае располагаются так (рис. 7.11), что через них можно провести три прямые линии: одну - через точки в интервале скоростей г = 20... 50 м/мин, другую - через точки в интервале скоростей г = 50... 105 nmhh и третью - через точки в интервале скоростей г > 105 м/мин. Каждая из. этих трех прямых может быть выражена своим уравнением, которые после потенцирования имеют такой общий вид: (7.17) Р = c j!; -.

Для каждого скоростного интервала числовые значения коэффициента с ( и показателя степени w( определяются по уже известной методике.

На заключительном этапе выводится общее уравнение функциональной зависимости P=fs{t, S, НВ, v). В каждом из предшествующих этапов эксперимента исследовалась степень влияния на силу резания Р только одного параметра при непременном условии постоянства всех прочих параметров. При этом в экспериментально найденных частных степенных зависимостях измеренное значение силы Р выражается как произведение двух сомножителей: постоянного коэффициента С( и переменного по значению независимого параметра х?. Найденные в экспериментах значения коэффициента с, на каждом этапе отражали влияние параметров, которые поддерживались постоянными и оказывали некоторое суммарное

воздействие. В то же время второй сомножитель х отражал влияние на значение Р только исследуемого на данном этапе фактора. Следовательно, значения показателей степени, найденные на предшествующих этапах, имеют общий характер и могут быть введены в обобщенное уравнение, в то время как значения коэффициента С( имеют частный характер и справедливы только в условиях эксперимента на каждом проведенном этапе. В связи с тем, что все полученные на предшествующих этапах частные функциональные зависимости однотипны и представляют собой степенные уравнения, обобщенное уравнение для нахождения силы резания Р может иметь следующий вид:

(7.18)

P = cptS{HB/200yv\

Числовое значение постоянного коэффициента Ср может быть найдено, если, разрешив это уравнение относительно постоянного коэффициента, т. е. ср = = i/[t S(HB/200) г ], подставлять в него взятые из протоколов конкретные сочетания полученных при проведении экспериментов значений силы резания и независимых факторов. Для увеличения точности вычисления значения коэффициента Ср берут некоторое количество п таких сочетаний (обычно достаточно п = 5... 10) и окончательно значение коэффициента Ср определяется как среднее арифметиче-

ское {ср = р /п

или среднее квадра-

тичное

значение.

§ 7.5. МОЩНОСТЬ И ЭНЕРГОЗАТРАТЫ ПРОЦЕССА РЕЗАНИЯ

МОЩНОСТЬ. Для разрушения материала срезаемого слоя и превращения его в стружку необходимо затратить некоторое количество энергии и произвести работу резания. Мощность, непосредственно затрачиваемая на осуществление процесса резания, называется эффек-