видно на рис. 10.3, в зоне малых скоростей резания v <V3 функциональная зависимость v(T) является возрастающей, т. е. с увеличением стойкости Г инструмента скорость резания также увеличивается, причем максимальная стойкость Гз достигается при скорости резания V3.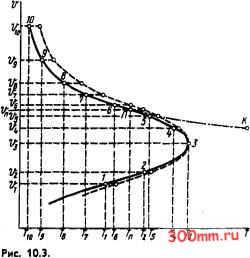

Общая мвисимость скорости резания V от стойкости Т инструменте

Во второй зоне при v> V3 зависимость v(T) убывающая.

На графике рис. 10.3 сплошной линией построена кривая для критерия равного износа, а пунктирной линией - для критерия оптимального износа. Из графика видно, что для обоих сравниваемых критериев износа существует общая закономерность функциональной зависимости v (г), и они отличаются друг от друга лишь количественно. Для обоих критериев допустимого износа зависимость скорости резания от стойкости инструмента имеет сложный нелинейный характер и общую точку максимальной стойкости Т3 при скорости V3. С уменьшением стойкости ниже значения г3 каждому ее значению соответствует два значения скорости резания - одного в области малых скоростей резания, а другого в области больших скоростей резания. При этом для равных скоростей резания стойкость инструмента всегда больше для критерия оптимального износа, чем для равного износа.

ПРАКТИЧЕСКОЕ ЗНАЧЕНИЕ СКО-

РОСТНЫХ ЗОН. Обработка металлов резанием возможна в пределах обеих скоростных зон от скорости 1 до скорости Vio и более. Однако резание с малыми скоростями V < V3, т. е. в пределах первой скоростной зоны, не рационально из-за низкой производительности труда и высокой цеховой себестоимости обработки каждой заготовки изготовляемых деталей машин. Обработка металлов с малыми скоростями резания может быть оправдана лишь необходимостью получения высокоточных обработанных поверхностей с высоким качеством поверхности.

Рациональнее обрабатывать металлы со скоростями V > V3, т. е. в пределах второй скоростной зоны. С увеличением скорости резания v, хотя стойкость инструмента Т уменьшается, сокращается также время обработки деталей, т. е. основное технологические время to и соответственно увеличивается производительность труда, в частности, на станках с ручным управлением.

Наиболее рациональное использование режущего инструмента достигается при обработке металлов резанием со скоростями, лежащими между скоростью v точки перегиба П и скоростью V3 точки максимума. Этот диапазон скоростей используют при назначении режимов производительной и экономичной обработки на автоматизированном металлорежущем оборудовании и автоматических линиях.

ЧАСТНАЯ ЗАВИСИМОСТЬ СКОРОСТИ РЕЗАНИЯ ОТ СТОЙКОСТИ ИНСТРУМЕНТА. Как уже было отмечено, при скоростях резания v> v ведут обработку металлов на универсальных металлорежущих станках. Важное практическое значение этого диапазона объясняет большой интерес, проявлявшийся к нему на ранних стадиях исследования, и обширный накопленный опыт. Это выразилось в разработке математического аппарата, предназначенного для аппроксимации частной функциональной зависимости v{T) для этого ограниченного диапазона скоростей.

На графике (рис. 10.3) этот диапазон наиболее часто применяемых на практике скоростей резания ограничивается наименьшей скоростью Dn точки перегиба П

и наибольшей скоростью Ью, Для которой стойкость Гю не должна быть меньше нормированного периода стойкости Г для данного вида и типоразмера инструмента. Для более детального рассмотрения на отдельный график (рис. 10.4) вынесен отрезок между скоростями v и ию кривой

Рис. 10.4. Частная зависимость скорости резания V от стойкости Т инструмента (в пределах Vr,...v, )

функциональной зависимости v = {Т}. Отрезок кривой на рис. 10.4 имеет более простую, чем вся кривая целиком, форму, сходную с гиперболой, и может быть аппроксимирован монотонно убывающей частной функциональной зависимостью. При практическом использовании этой зависимости иногда возникает необходимость выбора и назначения режимных точек за пределами диапазона ; ... fi о-В таких случаях следует учитывать, что экстраполировать по частной зависимости допустимо только в область скоростей v> Vn и не допустимо в область скоростей j; < v . На графике (см. рис. 10.3) видно, что экстраполированный отрезок ПК (показанный штрихпунктирной линией) резко расходится с кривой общей функциональной зависимости v(T) в области малых скоростей.

§ 10.3. АППРОКСИМАЦИЯ

ЗАВИСИМОСТЕЙ

СКОРОСТИ РЕЗАНИЯ

ОТ СТОЙКОСТИ

ИНСТРУМЕНТА

И РЕЖИМНЫХ ПАРАМЕТРОВ

Скорость резания, обеспечивающая заданную стойкость инструмента, определяется целым рядом факторов, в число

которьк входят глубина резания, подача и свойства обрабатываемого материала. Это справедливо как для общей зависимости, изображенной на рис. 10.3, так и для частной зависимости, изображенной на рис. 10.4. В связи с этим рассмотрим методику вывода на баЭе экспериментальных данных частной функциональной зависимости (для скоростей ;> ; ) v(T, t, S, НВ) в виде аналитического уравнения, пригодного для практического использования при разработке нормативных материалов.

ВЫВОД ЧАСТНОГО УРАВНЕНИЯ i; = Cj/T . Кривая на рис. 10.4 проведена как выравнивающая линия в поле разброса точек кривых износа, полученных экспериментально при проведейии стойкостных исследований. Аппроксимация этой зависимости ведется по точкам П ... 10. Она может быть выполнена на основе различных методов математической обработки и выражена различными по виду и ст{)уктуре математическими уравнениями. В данном случае кривая на рис. 10.4 имеет сходство с гиперболой, математически выражаемой степенным уравнением вида

(10.1)

j; = Ст/Т ,

где т - показатель степени, называемый показателем стойкости, а Cj- - коэффициент, значение которого зависит от всех, кроме скорости, факторов и параметров резания. Чтобы подсчитать по уравнению (10.1) скорость резания по заданной стойкости Т инструмента, необходимо знать числовые значения показателя стойкости m и коэффициента Cj. Они могут быть найдены двумя способами - аналитическим и графо-аналити-ческим, которые уже были описаны в гл. 7 при выводе зависимости силы резания от режимных параметров.

При использовании аналитического метода в уравнение (10.1) подставляют координаты i точек участка П ... 10 выравнивающей кривой и получают ряд уравнений у,- = Ст/ТГ, каждое из которых содержит два искомых неизвестных - m и Ст. Попарным делением из них исключается неизвестный коэффициент Cj, в результате чего можно получить 2i урав-

нений, с помощью которых после логарифмирования находят 2i значений показателя стойкости т. В случае незначительного (менее 10%) расхождения полученных значений т можно считать, что аппроксимация степенным уравнением возможна и правомерна. Тогда окончательное значение показателя стойкости т определяется либо как среднее арифметическое т<;р ар = X ДО. либо как среднее

квадратичное тр.в =

всех

найденных значений wij. Чтобы найти числовое значение коэффициента С, урав-нение(10.1) разрешают относительно этого коэффициента и в полученное уравнение вида Ст = VjTT вновь подставляют координаты точек выравнивающей кривой. Это позволяет получить i значений коэффициента Сп и окончательное значение коэффициента Стопределяется как среднее

арифметическое Сгср.ар = Z Tt/i или как

среднее квадратичное Стср.кв =

Существенное расхождение подсчитанных числовых значений т указывает на то, что кривая на рис. 10.4 не может быть удовлетворительно аппроксимирована степенным уравнением и для этой цели необходимо пользоваться уравнением другого вида.

При использовании графо-аналити-ческогоспособа по точкам участка П ... 10 кривой (см. рис. 10.4) производят построение зависимости в логарифмических координатах (рис. 10.5). Расположение всех точек на одной прямой служит доказательством, что кривая на рис. 10.4 может быть аппроксимирована степенным уравнением (10.1). Значение показателя стойкости т определяется из условия т = = tgxi =Значение коэффициента Ст определяется из условия v= Ст при Г= 1 (обычно принимают Г= 1 мин).

Если на графике с логарифмическими координатами деление шкалы, равное единице на оси абсцисс, отсутствует, то графический поиск значения коэффициента

Сг можно заменить аналитическим вычислением, используя графически найденное значение показателя стойкости т.

Принятый критерий допустимого из-

Рис. 10.5. Частная зависимость v(T) в логарифмических координотах: 1-для критерия равного износа; 2 - для критерия оптимального износа

носа инструмента влияет на значения эмпирических коэффициентов зависимости (10.1). Для равных условий резания линия 2 на рис. 10.5 соответствует критерию оптимального износа, а линия / - критерию равного износа. Поэтому в уравнении (10.1) числовые значения показателя стойкости т и коэффициента Ст всегда больше при использовании критерия оптимального износа, чем при тех же условиях резания при использовании критерия равного износа. Таким образом, высокие числовые значения показателя стойкости т и коэффициента Ст могут служить одним из признаков более полного использования ресурса инструмента.

ВЫВОД ЧАСТНЫХ УРАВНЕНИЙ v=C,/t; vCs/S ; v = С/ВВ При вьшоде частной функциональной зависимости V = Ст/Т использовались экспериментальные данные, при получении которых все параметры, обусловливающие процесс резания (кроме скорости резания v), поддерживались постоянными. Входящие в число этих параметров глубина резания t, подача S и твердость обрабатываемого материала НВ более, чем другие факторы, влияют на значение скорости резания, обеспечивающее заданную стойкость. Суммарное влияние их вместе с другими факторами задается коэффициентом Ст уравнения (10.1).

Многочисленные эксперименты пока-