зали, что при обработке конструкционных сталей в хдаапазоне скоростей резания t; ... Vio изменение глубины резания t, подачи S и твердости обрабатываемого материала НВ практически не влияет на числовые значения показателя стойкости т. Поэтому в логарифмических координа-

Рис. 10.6. Частные зависимости v(7) в логориф-мических координатах при различных значениях глубины резания

тах зависимость t; = C-rjT при разных значениях г, S и НВ имеет вид прямых линий, параллельных друг другу. На рис. 10.6 показано расположение семейства этих линий при различных значениях глубины резания t. Для установления функциональной зависимости vif) на графике рис. 10.6 можно провести вертикальную линию постоянной стойкости из произвольного деления шкалы абсцисс, например для значения стойкости Те. Точки 1, 2, 3, 4, 5, полученные при пересечении этой линии с линиями семейства прямых, дают возможность построить в системе логарифмических координат частную функциональную зависимость t; (t) (рис. 10.7). Практика исследований показала, что при обработке конструкционных сталей эта зависимость в логарифмических координатах выражается прямой линией и, следовательно, аппроксимируется уравнением вида (10.2)

Числовые значение показателя степени х и коэффициента С, в уравнении (10.2) находят аналитическим или графо-аналити-ческим способом, описанным выше. На рис. 10.7 показаны построения для опре-

деления показателя степени х = tg т = А/Б и коэффициента С, (С, = t; при t = 1).

Так как характер семейства кривых v{T) при различных значениях подачи S и твердости обрабатываемого материала НВ, как указывалось выше, подобен семейству кривых t; (Г) при различных значениях глубины резания t (см. рис. 10.6), то частные функциональные зависимости v(S) и i;(HB) выводят аналогичным образом. В результате можно получить эмпирические уравнения следующего вида:

(10.3) (10.4)

V = Снв/НВ

Каждое из уравнений (10.2), (10.3) и (10.4), как и уравнение (10.1), выражает зависимость скорости резания от одного параметра при сохранении остальных постоянными.

ВЫВОД ОБОБЩЕННОГО УРАВНЕНИЯ ЧАСТНОЙ ЗАВИСИМОСТИ

V [Т, t, S, НВ). Выше была изложена методика аппроксимации результатов экспериментов и вывод частных эмпирических уравнений, выражающих количественную зависимость скорости резания

V от основных факторов. В выведенном уравнении (10.1) в явной форме выражена зависимость скорости резания v от стойкости инструмента Т. Остальные факторы, в том числе глубина резания t, подача S и твердость обрабатываемого материала НВ, при выводе этого уравнения имеют постоянные значения и в совокупности определяют числовое значение коэффициента Cf В уравнении (10.2) в явной форме выражена зависимость скорости резания v от глубины резания t. Учитывая уравнение (10.2), можно вьщелить влияние глубины резания t на значение коэффициента Cj уравнения (10.1) следующим образом:

(10.5)

в уравнении (10.5) влияние глубины резания t выражено в явной форме, а коэффициент Ci выражает в скрытом виде влияние совокупности факторов, исключая стойкость Т и глубину резания t. Под-

ставив значение Ст в уравнение (10.1), получаем функциональную зависимость

V = CilVf.

Используя тот же прием, можно вывести обобщенное уравнение частной функциональной зависимости (для скоростей

Рис. 10.7. Зависимость скорости резания v от глубинь! резания t в логарифмических координатах

резания г > г ): (10.6)

где коэффициент CJ, (принятое обозначение в справочной и нормативной литературе) определяет влияние на скорость резания факторов, не входящих в данное уравнение в явном виде. К таким факторам могут относиться свойства инструментального материала, геометрия режущей части инструмента, использование смазывающе-охлаждающих жидкостей разных видов, жесткостные параметры оборудования и т. п.

Влияние твердости обрабатываемого металла на скорость резания v в уравнении (10.6) может быть выражено не абсолютным числовым значением НВ, а от-нощением НВ/200. Это делается для того, чтобы члены уравнений (10.6) имели сопоставимые по порядку числовые значения, поскольку отногпение НВ/200 мало отличается от единицы. Уравнение (10.6) в этом случае приобретает вид

(10.7)

V = C /[r tS(HB/200)i].

Числовые значения коэффициента С могут быть найдены также аналитически с использованием экспериментальных данных. Для этого уравнения (10.6) или (10.7) раз-

решаются относительно коэффициента Ci = гГ t S(HB)

С = гГ (НВ/200) 1.

Подставив в эти уравнения полученные при проведении экспериментов значения т, X, у к z(zi), можно получить значения коэффициентов С и С;,.

В производственных условиях значения коэффициента С (С,) и показателей степени т, X, у к z(zi) берут из таблиц, имеющихся в справочной литературе по металлообработке. В настоящей книге справочные таблицы приведены в главах, в которых рассматривается резание различными видами инструментов.

ПРИКЛАДНОЕ ИСПОЛЬЗОВАНИЕ ОБОБЩЕННОЙ ЧАСТНОЙ ЗАВИСИМОСТИ v{T, t, S, НВ). Рассмотренная зависимость, выраженная аналитическим уравнением (10.7), как указывалось, справедлива лишь для скоростей v > v .

Использование уравнений (10.6) и (10.7) основано на фундаментальном положении, что стойкость инструмента 7 всегда является аргументом, свободно назначается или выбирается по нормативным таблицам, а скорость резания v всегда является функцией и ее рекомендуемое значение вычисляется по этим уравнениям. При этом следует учитывать, что вычисленные расчетные значения скорости резания реализуются в редких случаях, поскольку металлорежущие станки имеют ступенчатое переключение частоты вращения шпинделя. Фактические скорости резания, осуществимые на станках, отличаются от расчетных, что влечет за собой соответствующее изменение стойкости инструмента, определяемое уравнением (10.1), разрешенному относительно стойкости:

(10.8)

Т = iCr/vV .

Здесь следует отметить, что при малых изменениях скорости резания, особенно вблизи точки перегиба П, стойкость инструмента, вычисленная по уравнению (10.8), может измениться весьма существенно.

§ 10.4. АППРОКСИМАЦИЯ

ЗАВИСИМОСТЕЙ

СТОЙКОСТИ

ИНСТРУМЕНТА

ОТ РЕЖИМНЫХ

ПАРАМЕТРОВ

Как было отмечено выше, при реализации рассчитанных значений скорости резания в зависимости от заданной стойкости инструмента, учитывая кинематические возможности станков, обычно возникает необходимость решения обратной задачи, а именно расчета фактической ожидаемой стойкости режушего инструмента. Кроме того, в ряде практических случаев расчет стойкости инструмента в зависимости от режимных параметров представляет собой самостоятельную задачу. В настоящем разделе рассмотрим методику вьшода зависимости стойкости инструмента от режимных параметров - скорости резания v, подачи S и глубины резания t.

ГРАФИЧЕСКОЕ ВЫРАЖЕНИЕ ЗАВИСИМОСТИ СТОЙКОСТИ ИНСТРУМЕНТА ОТ СКОРОСТИ. В рассмотренной в § 10.3 функциональной зависимости v(T) аргументом являлась стойкость Т, а функцией - скорость резания v. Поменяв местами координаты v м Т, получим кривую (рис. 10.8), графически выражающую функциональную зависимость T(v). Являясь зеркальным отображением кривой на рис. 10.3 относительно линии, про-ходяшей под углом 45° к координатным осям, данная кривая также нелинейна, имеет точку экстремума, в которой достигается максимальная стойкость инструмента Т, и точку перегиба J7.

По причинам, рассмотренным выше в § 10.2, рациональное резание достигается в диапазоне скоростей Vi ... Vio, в котором возможна практическая реализация организационно-технических требований, предъявляемых к рабочему режиму процесса резания, таких, как максимальная производительность труда, минимальный или нормированный расход инструмента, минимальная цеховая себестоимость и т. п.

АППРОКСИМАЦИЯ ЗАВИСИМОСТИ T(v). Для практического использо-

вания эмпирической зависимости T(v) (рис. 10.8) необходимо найти для нее аналитическое выражение. Поиск такого выражения является достаточно сложной задачей. Описывая графически интересующую нас закономерность, выбранная аналитическая функция должна предостав-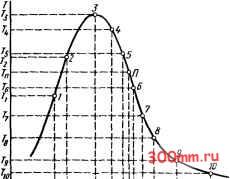

Рис. 10.8. Кривая зависимости Т (v)

лять возможность экстраполяции за пределы диапазона ее изменения при проведении данного эксперимента. При выборе типа формулы следует учитьшать также и особенности традиционного развития математического аппарата, используемого в области резания металлов. Так, например, здесь наибольшее распространение получили формулы степенного вида, позволяющие достаточно просто объединять частные уравнения, отражающие влияние отдельных факторов, в обобщенные уравнения, которые дают возможность найти значение искомого параметра при независимом изменении сразу нескольких факторов. Использование в этих, условиях иногда применяемых для аппроксимации эмпирических зависимостей многочленов п-й степени, тригонометрических функций или рядов может оказаться неудобным.

Учитывая эти требования, для аппроксимации зависимости T(v) было предложено уравнение вида

(10.9)

Т = CTie- .

Правая часть уравнения (10.9) представляет собой произведение степенной функ-