ции у = CiD* на показательную функцию у = Сге , где Сг = CiCj. Такое структурное построение придает уравнению (10.9) свойство описывать нелинейные экстремальные кривые, подобные линии на рис. 10.8.

На кривых, описываемых уравнением

В системе уравнений (10.10) неизвестными являются величины Cj, Ь и с. Исключив коэффициент Ст попарным вычитанием, получают два уравнения с двумя неизвестными fc и с. Решение системы уравнений позволяет найти показатель степени (10.11)

(Ig - Ig Г;+з)( (+1 - - (Ig Ti - Ig Ti+i){vi+3 - у,+г) (lgii+2 - lgi;i+3)(i>i+i - ii) - (Igii - Igii+iXfi+s - Vi+2)

(10.9), можно выделить характерные точки. Точка максимума имеет координаты Гтах и Vt = - Ь/Ст- Точка перегиба кривой Я имеет координаты 7 и v = (b +

--j/fc)/c [см. уравнения (9.23) и (9.24)]. Определив числовое значение скорости Гтах Р которой наблюдастся максимальная стойкость инструмента TJnax, по уравнению (10.9) легко подсчитать и само числовое значение максимальной стойкости Гщах- Рассчитав числовое значение скорости v в точке перегиба, можно определить нижний предел скоростной зоны, в которой допустимо практическое использование уравнений (10.6) и (10.7) частной зависимости v{T, t, S, НВ) при нахождении по ним допустимой скорости резания i; по заданной стойкости Т.

Аппроксимация результатов экспериментальных исследований состоит в нахождении числовых значений входящих в это уравнение параметров Ст, Ь и с. В специальной литературе, посвященной математической обработке экспериментальных данных, описаны различные методы решения этой задачи. Согласно одному из самых простых методов для определения указанных параметров удобно составить четыре уравнения, используя координаты четырех произвольно выбранных точек на кривой на рис. 10.8. Подставив координаты этих точек в уравнение (10.9) и прологарифмировав, получаем систему уравнений:

(10.10)

lg7; = igCT-l-blgi;i-ci;ilge; IgTJ+i = lgCr+blgii+i -ci+ilge; lgTi+2 = lgCT+blgvi-i- cv,+2lge; Ig Ti+3 = lgCT + blgD.+3 - cVi+3Ige.

и коэффициент (10.12)

(Ig Tj - Ig T,+1) - b (Ig vi - \gvi2) lge(f;, + i - Vi)

(Ig Ti+г - Ig Tis) ~ b{lgVi+2 -lge(i;j+3 - г.+г)

Разрешив уравнение (10.9) относительно коэффициента Ст, т. е. получив уравнение

(10.13)

Ст= Те /А

можно найти числовое значение этого коэффициента, подставляя в него найденные ранее значения Ь и с и координаты произвольной точки, взятой на кривой на рис. 10.8. Обычно для этой цели берут координаты точки максимума, т. е.

АППРОКСИМАЦИЯ ЗАВИСИМОСТИ T{v, S). Выше была рассмотрена методика аппроксимации зависимости T(v) по экспериментальным данным, когда все факторы, определяющие процесс резания (кроме скорости v), поддерживались постоянными. При изменении определяющих факторов кривая зависимости r(i;) может изменять как свою форму, так и расположение в системе координат Т - v.

Рассмотрим закономерности этих изменений и методику аппроксимации и вывода эмпирической зависимости, характерной для случая обработки конструкционных сталей инструментом из твердого сплава.

На рис. 10.9 в линейной системе координат показано семейство кривых r(i;), построенных по данным эксперимента при различных значениях подачи S, причем Si < S2 < s3 < < Sj. Из графиков на

рис. 10.9 видно, что: а) для всех значений подач сохраняется один и тот же вид функциональной зависимости T{v), аналитически выражаемый уравнением (10.9); б) с увеличением подачи S уменьшается количественное значение стойкости Т инструмента; в) для всех подач максимум стойкости 7;,ах имеет место при одной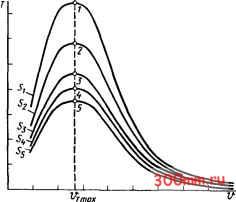

Рис. 10.9. графики зависимости Г(у) при различных значениях подачи

И той же скорости резания Vrl г) числовые значения показателя степени b и с и коэффициента Ст являются функциями подачи S.

Обработку экспериментальных данных с целью получения зависимости T{v, S) начинают с аппроксимации каждой кривой, построенной на рис. 10.9 согласно уже известной методике. Чтобы найти зависимость b(S), значения показателя степени Ь, вычисленные по уравнению (10.11), откладывают как точки в линейных координатах b - S и через них проводят выравнивающую линию (рис. 10.10, а). Эта линия может быть аппроксимирована уравнением

(10.14)

b = CTiSie-i .

Далее определяют числовые значения показателя степени bi и Ci и коэффициента Cjj соответственно по уравнениям (10.11), (10.12) и (10.13).

Аналогично аппроксимируют зависимости c(S) и Ct{S). Найденные при аппроксимации кривых T{v), изображенных на рис. 10.9, значения показателя степени

с и коэффициента Ст наносят на графики (рис. 10.10, б, в) и через них проводят выравнивающие линии. Эти линии могут быть описаны аналитическими выражениями (10.15)

с = Cy-jSze-iS (10.16)

Численные значения Cj-2, Ьг и Сг в уравнении (10.15), а также С, Ьз и Сз в уравнении (10.16) определяют по уравнениям (10.11), (10.12) и (10.13) с подстановкой в них значений точек, взятых с соответствующих кривых на рис. 10.10, б, в.

Обобщенное уравнение функциональной зависимости T{v, S) получают подстановкой в уравнение (10.9) найденных выражений показателя степени b и с соответственно по уравнениям (10.14) и (10.15) и коэффициента Ст по уравнению (10.16):

(10.17)

АППРОКСИМАЦИЯ ЗАВИСИМОСТИ T{v, S, t). Построение кривых зависимости T{v) при различных значениях глубины резания t показывает, что характер семейства кривых в этом случае такой же, как и при изменегши подачи S. На рис. 10.11 кривые построены при ti < t2 < 1з < и. Следовательно, как и в предыдущем случае, аппроксимируя кривые выражением (10.9), можно установить, что показатели степени Ьи си коэффициент Ст для разных кривых семейства зависят от глубины резания t. Обработав экспериментальные даннь1е, получаем аналитическую зависимость изменения показателя степени b от глубины резания t:

(10.18)

b = Cт4t e, изменения показателя с: (10.19)

с = С/5е-5;

изменения коэффициента (10.20)

Сг=СтбГе ь\

Обобщенное уравнение зависимости стойкости Т от двух параметров -. скорости резания и глубины резания - после подстановки уравнений (10.18), (10.19) и (10.20) в уравнение (10.9) примет вид (10.21)

пени Ь, напишем коэффициент Сп из уравнения (10.14) в виде

Ст-, = Cr,t*e-<

Подставив это выражение в уравнение (10.14), получаем

(10.22)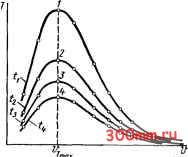

Рис. 10.1(3. Вид зависимостей показателей степени Ь и с и коэффициента Cj из уравнения (10.9) от подачи S

Тот же результат будет получен, если, учитывая влияние в явной форме подачи S на показатель степени Ь [см. уравнение (10.14)], записать Сг4 = CтSЧe- и подставить его в уравнение (10.18).

Так как на величины с и Ст- в уравнении (10.9) оказывают влияние подача S и глубина резания t и характер этого влияния описывается уравнениями аналогичного вида, то, произведя подстановки и преобразования, получим (10.23)

C=Cr9S2t5e-(<2S-<--5),

а зависимость Cr(S, t) - в виде (10.24)

Cr=Cr,oS 3t-6e- -

Подставив в уравнение (10.9) найденные выражения показателя степени b по уравнению (10.22), величины с по уравнению (10.23) и коэффициента Ст- по уравнению (10.24), находим обобщенное уравнение стойкости T{v, S, t):

(10.25)

~ CrsSt *

Рис. 10.11. Графики зависимости Т (v) при различных значениях глубины резо-ния

Выше бьшо установлено, что на значение показателя степени Ь в уравнении (10.9) одновременно влияют два параметра - подача S и глубина резания t. Для получения обобщенного уравнения T{v, S, t) необходимо поэтому найти зависимость b{S, t). Влияние на показатель степени b глубины резания t при проведении экспериментов с разными подачами S проявлялось в значении коэффициента Ст1 в уравнении (10.14). Равным образом влияние на показатель степени b подачи S при проведении экспериментов с разными глубинами резания отражалось на числовом значении коэффициента Ста в уравнении (10.18). Так как по уравнению (10.18) нам известно в явной форме влияние глубины резания t на показатель сте-