Если используются фрезы с винтовым зубом, в контакте с обрабатываемой деталью одновременно находится несколько режущих зубьев фрезы, причем в пределах поверхности резания некоторые зубья только вступают в работу, в то время как другие ее закан-

2 ~*rnDV

ный диаметр фрезы. Расстояние между смежными зубьями, измеренное вдоль оси фрезы (вдоль ширины фрезерования В), называется осевым шагом

h = В/к,

где к - коэффициент кратности, показы-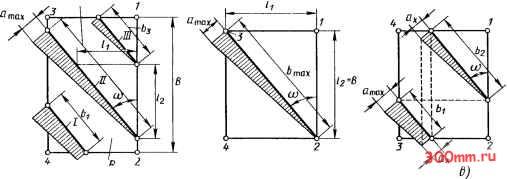

а) S}

Рис. 14.20. Условия равноперноГо фрезерования

чивают. Благодаря этому за счет режимных параметров и геометрии фрезы можно создать условия, когда суммарная толщина срезаемого слоя в любой момент времени будет постоянной, тем самым обеспечивая равномерность фрезерования.

УСЛОВИЕ РАВНОМЕРНОСТИ ФРЕЗЕРОВАНИЯ. На рис. 14.20,0 на поверхности резания R, изображенной в виде развертки на плоскость, показаны следы трех одновременно режущих винтовых зубьев /, и При вращении

фрезы каждый ее зуб начинает резание в точке 2. В это начальное мгновение ширина fc = О и толщина = 0. По мере вращения фрезы режущие кромки ее зубьев перемещаются справа налево по поверхности резания. Линии контакта зубьев с поверхностью резания на ее развертке имеют вид прямых, которые с осью фрезы образуют угол наклона со. Рабочий цикл каждого зуба заканчивается в точке 4.

Расстояние между смежными зубьями, измеренное в плоскости вращения фрезы, перпендикулярной ее оси, называется торцовым шагом

h = nD/z,

где Z - число зубьев фрезы; D - наруж-

вающий, сколько раз осевой шаг укладывается на ширине фрезерования.

Торцовый li и осевой I2 шаги связаны с углом наклона со винтового зуба фрезы соотношением

(14.9)

tgco = /i 2 = nfcZ)/(zB),

откуда

(1410)

к = zB tgco/(nZ)).

В частных случаях, когда осевой шаг фрезы один или более раз целиком и без остатка укладывается на ширине фрезерования В, коэффициент кратности k = B/l2 является целым числом; в остальных, более общих случаях коэффициент кратности к - число дробное.

При к2 хотя бы один из зубьев расположен так, что его след на развертке пересекает под углом со поверхность резания от линии 1-2 до линии 3-4 и, следовательно, ширина срезаемого слоя b для этого зуба максимальна (рис. 14.20, а). При к = I максимальная ширина слоя Ьтвх, срезаемого каждым режущим зубом, возможна при одном положении следа режущей кромки, когда на развертке он является диагональю развертки поверхности резания

(рис. 14.20,6). Значение максимальной ширины тогда определяется выражением

(14.11)

Ьтах = /i/sin СО = /2/cos со = B/cos со.

При дальнейшем перемещении режущей кромки по поверхности резания ширина срезаемого слоя b начинает уменьшаться. Вместе с тем после прохождения диагонального положения следа контакта рассматриваемого зуба в точке 1 поверхности резания в работу вступает очередной зуб и на поверхности резания располагаются следы контакта двух режущих зубьев (рис. 14.20, в). Далее при вращении фрезы длина следа первого зуба при перемещении его в пределах поверхности резания сокращается до нуля, а длина следа второго зуба при приближении к диагональному положению возрастает до максимума. Рис. 14.20,в позволяет убедиться в том, что при к = 1 суммарная ширина двух режущих зубьев в любой момент времени равна ширине Ь, одного зуба, занимающего диагональное положение.

Эпюра толщины срезаемого слоя, построенная вдоль ширины Ьгшх при к = = 1, содержит все мгновенные значения толщины от а. = О в точке 2 (рис. 14.20, б) до а, = в точке 5. На двух следах при коэффициенте кратности к = I эпюры толщины срезаемого слоя, построенные вдоль ширины bi на следе первого зуба и ширины Ьг на следе второго зуба (рис. 14.20, в), также содержат все мгновенные значения а, от нуля до а ах и сумма эпюр эквивалентна непрерывной эпюре одного

зуба, построенного вдоль ширины Ьалх-

Таким образом, при коэффициенте кратности к = 1 зубья фрезы, находящиеся в контакте с поверхностью резания, в любой момент времени срезают слой с постоянной площадью сечения, графически представленный одной непрерывной эпюрой а., построенной вдоль максимальной ширины Ь (рис. 14.20,6), или двумя эпюрами, построенными на соответствующих следах контакта шириной bi и Ьг (рис. 14.20, в). Аналогичные закономерности наблюдаются и при других целых значениях коэффициента кратности (к = 2, 3, 4 и т. д.).

Это условие постоянства суммарной

ширины и площади сечения слоя, срезаемого одним или несколькими зубьями фрезы при целых значениях коэффициента кратности к, принято определять как условие равномерности фрезерования, количественно выражаемое уравнением (14.9). Некоторые входящие в это уравнение величины (диаметр фрезы D, число зубьев z и угол со наклона винтовых зубьев) являются конструктивными элементами фрезы и могут иметь разные значения только при использовании фрез с разным конструктивным исполнением. При конструировании фрез, предназначенных для обработки заготовок с постоянной шириной фрезерования В, для обеспечения обработки с целым коэффициентом кратности к угол со наклона винтового зуба, удовлетворяющий условию равномерности фрезерования, рассчитывают по уравнению (14.9).

Ширина фрезерования В характеризует обрабатываемую заготовку. В условиях массового производства ширину В можно полагать величиной практически постоянной. В условиях единичного и серийного производства, когда происходит частая смена заготовок разной формы, основной причиной нарушения условий равномерного фрезерования является изменение ширины фрезерования.

Кратко суммируя изложенное, сохранить равномерность фрезерования можно, обеспечивая: а) целое число отношения ширины фрезерования В к осевому шагу /2 зубьев фрезы; б) постоянство суммарной ширины ЕЬ, срезаемой всеми зубьями фрезы одновременно; в) постоянство суммарной площади ЕЛ сечения всех одновременно срезаемых слоев.

ЗАКОНОМЕРНОСТИ НЕРАВНОМЕРНОГО ФРЕЗЕРОВАНИЯ. При невыполнении указанных выше требований обработка ведется в условиях неравномерного фрезерования. Наиболее важным показателем неравномерности фрезерования является переменное значение суммарной площади поперечного сечения слоев, срезаемых одновременно режущими зубьями фрезы. При неравномерном фрезеровании возникают неравномерные динамические нагрузки на фрезу и станок, что нежелательно с точки зрения точности обработки.

Площадь поперечного сечения слоя, срезаемого винтовым зубом при b = Ьах, в развертке на плоскость представляет собой прямоугольный треугольник (рис. 14.21), поскольку хотя линия 1-2 согласно уравнению (14.3) представляет собой отрезок синусоиды, но при х]/ 45° его можно

А А -OAmFr,ax

Рис. 14.21. Форма площади срезаемого слоя вдоль его ширины у фрез с винтовым зубом

Чтобы проанализировать закономерности периодического изменения суммарной площади LA при различных условиях неравномерного фрезерования, разобьем ширину срезаемого слоя Ь, на четыре равные части и вычислим площади сечения, соответствующие каждому отрезку Ь,1ах

/4 (рис. 1421). С помощью схемы на рис. 14.22 рассмотрим влияние ширины фрезерования В на закономерность изменения площади сечения срезаемого слоя LA за время поворота фрезы на один угловой шаг. На схеме показаны развертки поверхностей резания и находящиеся в контакте с ними следы режущих зубьев I и II при различной кратности к. При этом изменение к происходит только за счет

,b,7SB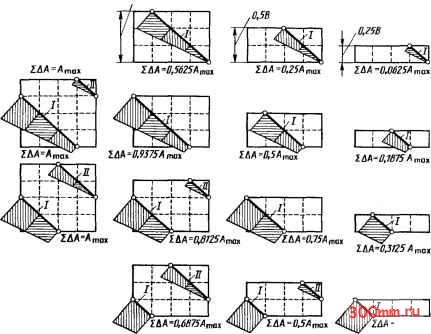

Рис. 14.22. Схема перемещения следов контакта лезвий по поверхности резания для различных значений коэффициента кратности:

о-(< = 1; 6-(< = 0,7S: e-(< = O.S; г~(< = 0,25

с некоторым приближением принять за прямую линию. Тогда площадь слоя, срезаемого одним винтовым зубом, равна

max Omaxmax

,bn,ax/2.

уменьшения ширины фрезерования при сохранении всех остальных параметров уравнения (14.9) постоянными. По вертикали в каждом столбце изображены четыре положения, соответствующие пово-