располагается выше горизонтальной характеристики пр р2=л/2. Из рис. 3.26 видно, что при заданной подаче тео ретический напор тем выше, чем больше рабочая лопасть отогнута вперед.

Достижение заданных теоретического напора и подачи-центробежной машины при рабочих колесах с различными углами требует различных окружных скоростей на выходе

из рабочего колеса или при одинаковом диаметре колеь различных частот вращения! Это ясно из теоретических ха* рактеристик, показанных на* рис. 3.27. .

Для получения заданного теоретического напора при одинаковом диаметре рабочих колес наименьшей частотой вращения должно обладать колесо с лопастями, загнутыми вперед, а наибольшей-колесо с лопастями, загнутыми назад.

По уравнению (3.74) можно выяснить форму характеристики теоретической мощности центробежной машины:

Лоо = MgH, = pQ (С - £Q) g. (3.75)

Эта характеристика может быть представлена графически для различных значений Рг при постоянных значениях р, п, Dz. bi.

На рис. 3.28 показаны теоретические характеристики мощности для углов Р2=20; 90 и 160°, при и = 1000 об/мин, Z)2=0,5 м и 2=0,03 м (центробежный насос).

20 30 W 50 а, Л/с

Рис. 3.28. Теоретические характеристики мощности при различных значениях угла pj

3.11. Действительные характеристики при постоянной частоте вращения

Действительный напор отличается от теоретического на значение потерь напора в проточной полости машины.

При изменении подачи машины потери напора меняются, во-первых, вследствие изменения сопротивления проточной полости, пропорционального квадрату средней скорости потока, во-вторых, по причине изменения направления скорости на входе в межлопастные каналы. Последнее

обусловливает удар жидкости (газа) о входные кромки лопастей и образование в потоке вихревых зон. В результате этого характеристика действительного напора располагается ниже характеристики теоретического напора.

В зависимости от значения лопастного угла Pz и конструктивных особенностей проточной полости центробежной машины действительная характеристика может иметь две типичные формы.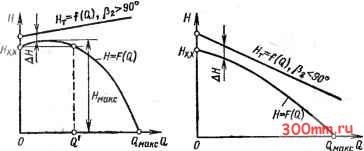

Рис. 3.29. Действительная характеристика при Р2>40°

Рис. 3.30. Действительная характеристика при P2<40f

Характеристика, представленная на рис. 3.29, типична для Р2>40°. Особенностью такой характеристики является наличие максимума и, следовательно, неоднозначность зависимости H=f{Q) для данной машины в пределах напоров от Ях.х до Ямакс Машины с характеристикой такого типа, как позднее будет показано, могут работать цеустой-чиво, самопроизвольно изменяя подачу. Это является отрицательным свойством машины, и поэтому такой тип характеристики нежелателен.

Другая форма характеристики, представленная на рис. 3.30, свойственна центробежным машинам с Р2<;40° прн рациональной конструкции проточной части.

Действительная характеристика мощности машины Может быть получена из теоретических характеристик путем вычитания (при данных подачах) из значений теоретической мощности ее потерь. При этом характер зависимости мощности от подачи в основном сохранится: действительная мощность машины будет возрастать с увеличением Подачи. Однако вследствие неодинакового относительного влияния потерь на полную мощность линия действительной Мощности отклоняется от линии теоретической мошно-

сти; она представится слегка изогнутой кривой, Теорета, ческая мощность при подаче, равной нулю, также равн нулю. Действительная же мощность при Q=0 (при закрц. том дросселе) равна мощности холостого хода Ni,i, затра. чиваемой на покрытие потерь мощности в этом режиме. По. терн мощности на холостом ходу обусловлены циркуляца. онными потоками в проточной части машины, особенно ц рабочем колесе, дисковым трением о жидкость (газ), мь ханическим трением в уплотнениях и подшипниках маши-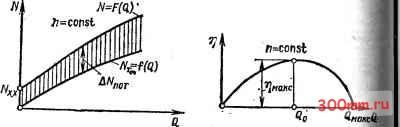

Рис. 3.31. Характеристики теоретической и действительной мощностей центробежной машины

Рис. 3.32. Характеристика КПД центробежной машины

НЫ. Все указанное приводит к форме характеристик действительной мощности, показанной на рис. 3.31.

По характеристикам действительного напора и дейс .,вительной мощности определяется КПД центробежно машины. Из уравнения (2.9) получим

1000Л/

Очевидно, КПД равен нулю при Q=0 или Н=0, потому что при всех режимах работы машины Ло. В пределах между Q=0 и Q=Смаке (рис, 3.32) КПД машины достигает максимального значения.

Режим машины, при котором ее КПД максимален, называют оптимальным; при этом затрата мощности для создания напора и подачи осущ(ествляется в машине с наилучшим энергетическим эффектом, т.е. наиболее эконо-

мично

Напоры (давления), подачи и мощности, приводимые в справочниках, относятся, если нет оговорок, к оптимальному режиму машине

3 12. Подобие центробежных машин. Коэффициент быстроходности. Формулы пропорциональности

Движение жидкостей (газов) в проточной полости машины весьма сложно. Поэтому точный расчет рабочих элементов машины представляет большие трудности. При проектировании насосов и компрессоров широко используют опытные данные, полученные при исследовании машин, аналогичных проектируемой. Использование опытных дан-

-1-зг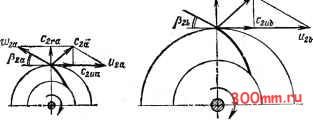

Рис. 3.33. Параллелограммы скоростей подобных центробежных машин

ных при проектировании допустимо лишь при соблюдении законов подобия.

В современном гидромашиностроении широко применяется метод моделирования, т. е. испытания моделей, позволяющий проверить проект и внести в него практические коррективы. Модели строят, как правило, с соблюдением законов подобия.

Физические явления, протекающие в геометрически подобных пространствах, называются подобными, если в соответственных точках этих пространств сходственные физические величины находятся в постоянных соотношениях. Эти соотношения называются коэффициентами или масштабами подобия.

Пусть машины а и b (рис. 3.33) подобны. Условия геометрического подобия этих машин заключаются в равенстве сходственных углов и постоянстве отношений сходсг-венных геометрических величин:

Рю == Pi6 = Рга = Ргь = Рг. Pia = Ргь = Рг? ]

Dia bia ha

где б, - коэффициент геометрического подобия.

Кинематическое подобие состоит в постоянстве отноше. НИИ скоростей в сходственных точках геометрически подоб! ных машин и равенстве сходственных углов параллело-граммов скоростей:

1а = 1ь; 20 = 2ь; -; i = *ь;

=-i =- =-i = ... == 6, = const,

la Ща . Cia С,а

(3.77)

где бс - коэффициент кинематического подобия.

Динамическое подобие выражается постоянством отношений сил одинаковой природы, действующих в сходственных точках геометрически и кинематически подобных машин:

Pib

: const, (3.78),

где бр - коэффициент динамического подобия.

Из изложенного следует, что доказательство подобия течений в двух насосах заключается в обнаружении постоян-ства коэффициентов подобия для сходственных точек.

Если известны коэффициенты подобия двух машин, та по известным характеристикам одной машины ha, р,а, Сщ Pia можно получить значсния сходственных характеристик другой машины:

Общие критерии подобия потоков, известные в гидроаэромеханике как числа Рейнольдса, Фруда, Эйлера и Стру-хала, применимы и к потокам в центробежных машинах. Напомним выражения этих чисел через основные парамет- ры потоков: Re=c v, ET=clgl; Eu=p/pc; Sh=/n/c.

Подобие течений характеризуется следующими равенствами безразмерных критериев, вычисленных для сходственных точек машин:

Ке = Кеь; Еи = Ец

Sh = Shb

(3.79)

Для компрессоров число Эйлера выражают через местную скорость звука а и показатель адиабаты k, между которыми существует зависимость a=Vkplp. Следовательно, p=ap/k, и поэтому

Безразмерную скорость с/а обозначают через М. Тогда £0 = 1/(fcM), откуда следует, что для подобных компрессоров М = Мб.

Таким образом, условия подобия компрессоров выра-5каются следующими равенствами:

М = М,;

Sh = Sh

(3.80)

Поскольку в процессе работы компрессоров проявляется теплоотдача, для строгого соблюдения подобия следует сохранять еще и постоянство критериев Прандтля и Грас-гофа.

Заводы, изготовляющие центробежные машины, обычно имеют в производстве не случайные типы машин, различающиеся и размерами, и геометрической формой, а серии геометрически подобных машин. Поэтому важно установить соотношения между основными параметрами машин данной серии.

Предположим, что две подобные машины а к Ь с радиальным входом работают в подобных режимах (см. рис. 3.33). При этом должны соблюдаться условия кинематического подобия [см. (3.77)].

Объемная подача для обеих машин

QbDbbCzrbnob-

Рассмотрим отношение этих подач:

Из подобия планов скоростей на выходе и условия пропорциональности окружной скорости частоте вращения рабочего колеса машины следует

Поэтому

Qa

2а Ьга а

Вследствие геометрического подобия машин