следовачельно, в окончательном виде

2а Па 1оа

(3.81)

Объемные подачи центробежных машин, работающих в подобных режимах, относятся как кубы наружных диамет-ров рабочих колес и первые степени частот вращения валов и объемных КПД.

Если рассматривается центробежная машина данного размера, то D2a=£>2b и, следовательно,

Qa Па Г\оа 3 ggj

При изменении частоты вращения вала центробежной машины объемные подачи ее в подобных режимах относятся как первые степени частот вращения вала и объемных КПД.

Пользуясь соотношениями (3.15) и (3.18), получае

Щ.а 2ua го

26 C2ub 1г&

По условиям кинематического подобия-2-=. Кром

того.

2а

следовательно,

а

(3.83)

Полные напоры, создаваемые центробежными машинами в подобных режимах, относятся как квадраты наружных диаметров рабочих колес, квадраты частот вращения вала и первые степени гидравлических КПД.

Для данной машины при переменной частоте вращения

Яа а Ira

(3.84)

При изменении частоты вращения вала центробежной машины напоры, создаваемые ею в подобных режимах, оЧН носятся как квадраты частот вращения вала и первые степени гидравлических КПД.

Соотношение между давлениями, создаваемыми машинами, получается умножением обеих частей уравнения (3.83) ра соответственные значения плотностей:

Ра Ра Ид

РьНь

(3.85)

Для данной машины при разных частотах вращения ее вала

Ра Ра Пг

п1 Рь гЬ

(3.86)

Давления, создаваемые центробежной машиной в подобных режимах, пропорциональны плотности перемешаемой ею среды (жидкости или газа).

Из формулы для расчета мощности на валу центробежной машины следует

Ра Qa gHa

Соотношение между мощностями на валах двух центробежных машин, работающих в подобных режимах,

Ng PgQaHa4b

PbQbHtV,

Учитывая выражения (3.81) и (3.83) получаем

Na Ра ЧЬ

Pb *1а

(3.87)

Мощности центробежных машин, работающих в подобных режимах, относятся как пятые степени наружных диаметров рабочих колес, кубы частот вращения валов, первые степени плотностей перемещаемых машинами сред и обратно пропорциональны КПД.

При небольшой разнице в размерах и частотах вращения машин можно полагать г]а=г\ь-

Для данной машины, подающей несжимаемую жидкость (вода, нефтепродукты, растворы), ра = рь; D2a = D2b и формула (3.87) приобретает простейший вид

(3.88)

Соотношения (3.82), (3.84), (3.88) называют формулами пропорциональности. Для удобства пользования иЗложеи-

ным материалом ниже приведены формулы пропорщ нальности при изменении параметров Q, И, р и N:

I~Il}H ИЗМбИбНИЯК

Лрп изменениях D п и р При изменениях Р D, РН пзмененпяц

Qa = Qb-

2a a

2a a Po Пга

Ра=РЬ -Г ----

Zj 4 Рь Чгь

Ра lb

а=пь~.----

d4 4, Рь la

РаРЬ

Dlb Dlb

Qb- ч

2a

Pa = Рь-

Na = Nb

Применяя формулы пропорциональности, можно прини-мать КПД машин, работающих в подобных режимах, прак-тически одинаковыми.

При строгих расчетах следует иметь в виду некотороа повышение КПД при увеличении размеров машины. Не сле дует, однако, думать, что пересчет Q, Н f\ N по формулам пропорциональности приводит к правильным результатам независимо от условий, в которых работает центробежная машина. Работа машины определяется также свойствами трубопроводной системы, подключенной к ней. Поэтому определение основных параметров Q, Н и N машины, включенной в трубопроводную систему, должно производиться, как указывается ниже, с учетом рабочих свойств последнее

Важной величиной, определяющей подобие течений в насосах, является коэффициент быстроходности tis.

Коэффициентом быстроходности данной машины (насоса, вентилятора, компрессора) называют число, равное частоте вращения машины, геометрически подобной данной, но имеющей подачу Q = l mVc и напор Я=0,102 Ы (соответственно L=gH = \ Дж/кг) в режиме максимального КПД.

Полагая в уравнениях подобия (3.81) и (3.83) Q=l м*/* и gH= 1 Дж/кг, получаем

Q V 02 /

(3.89)

(Г(4)

решение этих уравнений дает

Коэффициент быстроходности п - безразмерная величина, являющаяся коэффициентом подобия. Однако в практике насосостроения в качестве коэффициента быстроходности до настоящего времени применяют размерную величину

, = 3.65-. (3.92)

отнесенную к единичным величинам Н = 1 м; Л=1 л. с. Формула (3.92) получается из условий подобия (3.81), (3.83), (3.87).

Понятие ris по (3.92) перешло в насосостроение из области гидротурбостроения, где в качестве единичных эталонных величин были приняты Н = 1 м, Л=1 л. с и следующий отсюда единичный расход Q = 0,075 м/с.

Коэффициент быстроходности tis определяется величинами Q, Н и п; при регулировании машины он может изменяться в пределах от О до оо.

Характеризуя машину при помощи Us, обычно относят его к режиму с максимальным КПД.

Значения Пв для различных типов насосов следующие:

Ротационные и поршневые............ <40

Вихревые................... 10-40

Центробежные................. 4С-300

Диагональные.................. 300-600

Осевые.................... 600-1200

При помощи коэффициента быстроходности, вычисленного по выражению (3.92), можно выбирать тип машины Для работы с заданными Q, Н и п.

По предложению ЦАГИ коэффициентом быстроходности вентилятора принято считать частоту вращения вентилятора данного типа, который в режиме максимального ПД подает 1 м/с ra3aj создавая условное давление 30 кгс/м. Тогда rts= nVq IH, где Н - напор, приведенный к р= 1,2 кг/м.

3.13. Пересчет характеристик при изменении частоты вращения машины и вязкости среды

Влияние частоты вращения на характеристики насоса.

Задана характеристика H = f{Q) насоса (вентилятора) при частоте вращения а (рис. 3.34).

Требуется перестроить эту характеристику на Другую частоту вращения пь>Па, полагая гидравлический и объ, емный КПД не зависящими от частоты вращения.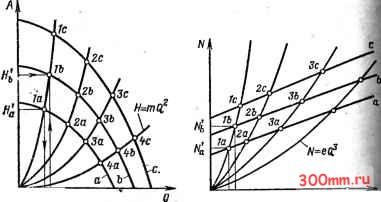

Рис. 3.34. Построение характери- Рис. 3.35. Построение характери-cfHK H=f{Q) по формулам про- стик N=f{Q) по формулам про-

порциональности

порцнональности

Из формул пропорциональности следует

Иь=-На

Выбрав на характеристике а произвольную точку 1й, находим на осях координат численные значения Q и Яд. Затем вычисляем координаты точки 16 (характеристики для

частоты вращения пь) Qb=Qa и °

о а

ЭТИМ координатам наносим на графике точку lb.

Аналогично по координатам произвольно выбираемых точек 2с,3с,4а... вычисляем координаты точек 2b,3b,4b...- наносим эти точки в график. Соединяя их плавной линией,

получаем характеристику H=f{Q) для частоты вращения вала Пв. Точно так же можно построить 1с, 2с, Зс... характеристики при частоте Пс и других частотах. Соединив точ-

la, lb, Ic..., 2с, 2b, 2с..., За, ЗЬ, За..., получим параболические кривые, удовлетворяющие уравнению H=mQ, называемые линиями пропорциональности (т - коэффициент пропорциональности уравнения квадратичной параболы).

При пересчете координат КПД машины полагался постоянным, не зависящим от частоты вращения. Поэтому линии пропорциональности являются линиями постоянных КПД машины.

Очевидно, точки пересечения линий пропорциональности и характеристик H=f{Q) при разных частотах вращения определяют параметры Q и Н машины в подобных режимах работы.

Пересчет характеристик N=F{Q) проводится аналогичным способом по формулам пропорциональности

Qb=Qa

По координатам Q, Q, Q ... и Л;, ЛГ, N ... произвольно взятых точек 1а, 2а, За... получим пересчетом координаты точек lb, 2b, 3b... и Ic, 2с, Зспо которым проводим кривые зависимости мощности от подачи при частотах вращения пь и Пс (линии Ь и с на рис. 3.35).

Линии 1а, lb, 1с..., 2а. 2Ь, 2с... являются линиями подобных режимов с постоянным для каждой из них значением КПД. Общий вид уравнения этих линий

где е - коэффициент пропорциональности уравнения кубической параболы.

Следует иметь в виду, что в общем случае работы машины на сеть, напор которой подчинен уравнению Я= ст + + Q, КПД машины при изменении режима не остается Постоянным. Условие т] = const при изменении частоты вращения соблюдается только в том случае, когда напор в сети Подчинен законам квадратичной параболы H = mQ, т.е. в Сети нет статического напора.

Выясним, как изменяется форма характеристики КПД fiQ) при изменении частоты вращения (рис. 3.36). Дд-Чь1 характеристики напора и КПД при частоте вращения а (кривые показаны сплошными линия.ми). Проведем ли-