и d1

лено в случаях, когда известна зависимость между р и р, т. е. когда известен термодинамический процесс в межло4 пастном канале машины. В машинах низкого давления!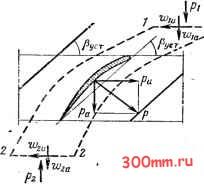

Рис. 6.4. Применение reopeJ мы импульсов к определ нию сил, действующих jiS лопасть

(вентиляторы) -это изотермический, а в осевых компрес-3 сорах - политропный процесс. i

Энергия, сообщаемая потоку рабочей лопастной решет-, кой, может быть рассчитана по основному уравнению центробежной машины, в котором щ=щ=и:

т = (с2 -С1 ) = Дс . I

Из планов скоростей (рис. 6.3) следует 1

ги = 2 - Саа ctg Ра . Хи = i - Ci ctgP.

Подставляя значения Сги и Сщ в выражение используя выражение (6.5), получаем

L, = c (ctgPi-ctgP2).

для Lt и

(6.7)

Уравнение энергии абсолютного движения через рабочую лопастную решетку осевой машины можно записать аналогично уравнению (3.20):

:(ctgPi-CtgP2) = Cp(r2-rO +

+ q. (6.8)

Уравнения количества движения. Уравнения количества движения служат для расчета сил взаимодействия между потоком и лопастями осевой машины. Пустьучасток ло- пасти длиной Дг действует на поток с силой Р (см. рис. 6.1 и 6.4). Проекции этой силы: Ра - на ось машины и Р - на ось решетки. Рассмотрим поток при относительном движении с шириной, равной шагу решетки.

Через сечение 11 проходит в секунду масса lS,rtWiaPi, (бладающая в направлении оси машины количеством дви-

ЧСНИЯ riWiapxWia, ЗНаЛОГИЧНО для сечения 2-2 ArtWiaPlWia-

Если р и Рг -давления в сеченнях 1-1 и 2-2 потока, то обусловливаемые ими силы.- соответственно Аг/р, и

Импульс внешних сил, действующих на поток в направлении начальной скорости, равен изменению количества движения потока, поэтому

(Р -f Мр ~Мр,) 1с =~ (АгР2< Artp, <}.

Знак минус в правой части равенства указывает на то, что изменение количества движения рассматриваемого объема жидкости вызывает силу, действующую на лопасть Б направлении, обратном Ра. Следовательно,

= Art {р, - р,) + Art (р, wl - р, wl). (6.9)

Для несжимаемой жидкости pi=p2 и по уравнению

(6.5) Wia = W2a, ПОЭТОМу

Р = А/(Р2-Р,). (6.10)

Решетка профилей, перемещающая несжимаемую жидкость, не изменяет осевой скорости потока; осевая сила, приложенная к потоку, расходуется на повышение давления.

Применим уравнение количества движения для определения тангенциальной составляющей Рц. Для этого запишем уравнение количества движения в проекции на ось решетки.

Количество движения в сеченнях /-/ и 2-2

ArtWia Pi ВУ1 и Аг/Ш2 р2 W.

Уравнение количества движения

Р 1с = - {ArtW2a Р2 Щи - р1 1 и)-

Отсюда следует

Р = Art (р, Ш1 - Рг Wza Wzu).

Используя равенство (6.4), получаем

Р = Дг/р, (tt i - WzJ. (6.11)

Результирующая получается геометрическим сложением сил Ра и Ри.

Уравнение циркуляции. Общее выражение для цирку ляции

с COS а ds

легко применяется к профилю решетки. Рассматривая кс тур 1-1-2-2-1- (си. рис. 6.4), представляем циркуляцию ка сумму следующих интегралов:

12 2 1

Г= 1 Widt+ 1 ffi ds- f rff - f СУ ds.

1 1.2 2

Ввиду того что линии 1-2 и 2-7 геометрически одинаковы] и скорости в соответственных точках равны второй и че вертый интегралы сокращаются. Следовательно,

Г= J(al -Ш2J Пocкoлькy Wiu и W2U - постоянные, средние по шагу величины,

T = {w ~w,)t. (6.12)j

Tec-рема Н. Е. Жуковского. Подъемная сила лопасти Cj 1=1, движущейся в неограниченном пространстве, опре деляется известной теоремой Н. Е. Жуковского

Р, = ршГ, (€.11

где W - относительная скорость набегающего потока; Г-j циркуляция по контуру, охватывающему лопасть. j

Изолированная лопасть не изменяет параметров пото: ка: относительная скорость перед лопастью и за нею одинакова. Решетка лопастей, как это видно на рис. 6.3, изменяет значение и направление относительной скоростям {хюхфхю). В этом заключается существенное различие bi действии изолированной лопасти и решетки лопастей на; поток. \

Теорема И. Е. Жуковского для лопасти решетки . 1

Py = 9Tw. (6.!

Из рис. 6.3 ясно, что Waa предстявляет собой среднюк ! ректорную скорость

В случае обтекания решетки газом плотность р в уравнении (6.14) можно полагать среднеарифметической плотностей входа и выхода.

Нетрудно убедиться, что направление силы Ру нормально к вектору Шоо (рис. 6.5).

Аэродинамические коэффициенты. Распространяя известный в аэромеханике способ расчета сил, действующих

Рис. 6.5. Силы, действующие со стороны лопасти на поток

Рис. 6.6. Результаты испытания решетки при малых скоростях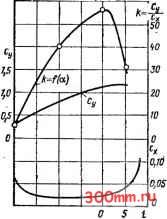

-zv-rs -го -S

на изолированную лопасть, на решетку профилей, можно записать

(6.15)

Такую лопасть называют изолированной.

где Су и Сж - коэффициенты подъемной силы и лобового сопротивления; Ру и Рх - подъемная и лобовая силы взаимодействия потока и профиля решетки.

Коэффициент Сх может быть определен только опытным путем; приближенное значение Су можно найти теоретически, а точное - из опыта.

Сопоставив уравнения (6.14) и первое из уравнении (6.15), получим

Следовательно,

Последнее уравнение совместно с уравнением (6.12) no3i ляет определить Су.

Из рнс. 6.3 имеем

Поэтому

= ctg р, sin Р=х> и ctg sin Рсо.

c,= 24-(ctgpi-ctgp,)sinp

(6.16)

Это равенство дает возможность расчета коэффициента с, по известным параметрам решетки профилей.

Точные значения и Су получают путем продувки решеток лопастей различных форм при разных углах атаки производя измерения скорости, плотности и сил Ру и Рх, производят расчет Су и Сх по уравнениям (6.15). Результа ты продувок изображают графически, как это показано, например, на рис. 6.6.

Подобрав при проектировании диаграмму для решеткц данного геометрического типа и задавая угол атаки, находят по диаграмме значения с и Сх и по формулам (6.15) вычисляют Ру и Рх.

6.3. Напор, потери энергии, КПД

Теоретический напор, создаваемый рабочим колесом-осевой машины, может быть вычислен по уравнению Эйлера, в котором следует полагать ui-Ui=u. При этом условии получаем уравнение (6.7). Введем в это уравнение Коэф фициент расхода ф:

Ф = с>, (6.17)

определяющий объемный расход, приходящийся на едини-! цу площади поперечного сечения решетки лопастей.

Тогда получим

Я, =cЛctgPl-ctgP,) = -ф(ctgP,-ctgP2). (6.18)1

Теоретическое давление, создаваемое колесом.

Pi = PgH = Р Ф (ctg Pi - ctg Рг). (6.19)

Потери энергии в осевых машинах обусловливаются трением и вихреобразованием в проточных полостях, перетеканием части потока через зазоры, механическим трением в подшипниках и уплотнениях.

Эффективность решеток осевых машин для несжимаемой жидкости момчет оцениваться посредством КПД решетки

(6.20)

где р и Рт - действительное и теоретическое повышения давления в решетке; Др - потери давления в решетке. Если решетка повышает давление.с pi до Рг, то

Рг - Pi + Др

Для несжимаемой жидкости по уравнению (6.6)

(6.21)

P2 - Pt + P = 9-

v\-wl

(6.22)

Из планов скоростей входа и выхода следует

te)j - И)

р(!ЗУ1 -ayaJjjyctgPoo,

где Роо - угол между вектором и осью решетки. Используя выражение (6.22), получаем

P2-Pi + Ap = -7ctgP ,. ,

По уравнению (6.10) для решетки с Дг=1

P2 - Pi==PJt.

Следовательно,

% = -:-cteP = j-.

(6.23)

В соответствии с рис. 6.7 Ра = Ру COS Рсо - Рх sin рос; Р = Рх cos р + Ру sin Рсо. (6.24)