Пусть через колесо машины проходит расход Q кости или газа с постоянной плотностью р; моменты кс честв движения, отнесенные к 1 с, составят pQcii на де и PQC2I2 на выходе из колеса. Здесь pQ - массо расход через колесо; ci и Сг- абсолютные средние скс сти потока на входе и выходе межлопастных каналов; h - плечи скоростей Ci и Сг (рис. 3.2).

Если обозначить Мтоо теоретический момент, переда емый потоку с вала (в предположении бесконечного кс честна лопастей и при отсутствии потерь в процессе пр< разования механической энергии в гидравлическую), уравнение моментов количеств движения для времена с. будет иметь вид

Мтоо Д i = {pQcJz - PQcik) Д t.

Момент, подводимый от двигателя к валу мапп больше Мтоо вследствие механического трения в подшиг ках и уплотнениях вала, наличия объемных потерь и ния нерабочих поверхностей колес о жидкость (газ).

Введем в уравнение (3.2) конструктивные радиусы 2: /i=?icosai; /2 = y?2Cosa2, тогда

Мтоо = pQ (Rz cos 2 - cos tti).

Здесь ai и a2 - углы между абсолютными и переноснь скоростями на входе и выходе.

По рис. 3.2 CiCosai = Ci ; C2COsa2=C2u, следовательнс

Мощность, передаваемая потоку в межлопастных щ лах,

Лтоо = Мтоссо = р Q (Rzu - Л ) ю,

/Vtoo =pQ( aC2 - iCi ).

Теоретическая мощность при бесконечном количг лопастей может быть вычислена и как произведение сы, проходящей через рабочее колесо в секунду, на ветствующую уделЬную работу:

Лтоо = PQLtoo.

Из сопоставления (3.5) и (3.6) следует

Z-Too = tizu - %ltf

Удельная работа связана с напором равенством (2.6), J которого с учетом (3.7) следует

gToo === uzu - Ли-

{поэтому

Ятоо == ( гСги - (3.8)

Теоретическое давление ртоо получается из (3.8) и из-Ir.ecTHoro соотношения гидромеханики р=\Н, где y=pg - [удельный вес среды,

Ртоо = р (и2и - 4i(iu)- (3.9)

Уравнения (3.4), (3.5) и (3.8) - основные уравнения [центробежной машины. Уравнение (3.8) было получено [великим математиком Леонардом Эйлером в 1754 г. н на-[зывается уравнением Эйлера.

При использовании основных уравнений скорости Ci и \с2и по окружностям радиусов Ri и R2 принимаются постоянными, так же как и прочие составляющие параллело-[граммов скоростей на входе и выходе. В действительности [это не так, потому что лопасти, развивая силу взаимодей-{ствия с потоком, должны по теореме Жуковского о подъ-[емной силе крыла иметь положительное значение циркуляции, что имеет место только при разных значениях относительной скорости на выпуклой (рабочей) .и вогнутой (нерабочей) поверхностях лопастей. Таким образом, относительная скорость в межлопастных каналах должна изменяться от наибольшего значения на вогнутой стороне лопасти до наименьшего значения на выпуклой, а не оста-I ваться постоянной.

В изложенном заключается парадоксальность рассмот-ренной струйной теории центробежной машины. Из параллелограммов на входе и выходе следует

w\ = ui -f ci--2ыс, ;

w] = u] + cl - 2uzu-

Определив отсюда лроизведения UiCm и uqCzu и внеся порученные выражения в (3.8), получим уравнение

ul- и\ Нтоо = ---h

2 22

wi-oih C - Ci

(3.10)

Первый член этого уравнения - напор, обусловленный работай центробежной силы жидкости (газа).

3-559 , 33

Члены уравнения (3.10) {w\-wl)/2g и (С2-c?)/2g ражают, очевидно, прирост напора вследствие преобра вания кинетических энергий относительного и абсолют1( движений в межлопастных каналах.

Скоростной напор, создаваемый лопастями рабочего леса, при принятых ранее допущениях равен

iHjroc{cl-cl)l(2g), (3.

потому что абсолютная скорость потока повышается ко. сом от ci до Сг. Поэтому теоретический статический Hai, составит

ст)т< - Ятоо- (£/ск)тоо --г- -Ь

2g 2g

Из последнего равенства следует, что повышение тического напора и давления лопастным колесом це бежной машины происходит за счет работы центробея сил и понижения кинетической энергии относителы движения.

Если выполнить межлопастные каналы так, что н: чение по всей длине будет постоянно, то Wi = W2 и тео ческое статическое давление, развиваемое таким кол

(Рст)тоо = р(и2-и?)/2. (

Тангенциальная составляющая абсолютной ско ciu характеризует закрученность потока перед входо: межлопастные каналы. Удельная работа, затрачивав] на закручивание, численно равна iCi , Дж/кг; она пер ется жидкости и суммируется с работой, передаваемой току рабочими лопастями. Поэтому в соответствии с (i удельная теоретическая энергия потока на выходе из бочего KOJtfeca

Следовательно, при определении теоретических па метров машин, не имеющих на входе специальных тройств, закручивающих поток, основные уравнения п ставляются в следующем виде:

Мхоо = р QRi; = u2ut I

Равенства (3.15) обычно называют основными урав киями центробежной машины с радиальным входом ciu=0 абсолютная скорость радиальна).

Из треугольника скоростей на входе при Ciu = 0 следует

2; поэтому уравнения (3.10) - (3.12) дают сле-

щне, характерные для машин с радиальным входом зна-ения теоретических напоров:

= iul-wl+cl)/{2g);

too

{Hc )roo = {cl-cl)/(2gy,

{H )r< = U-W2+Cm2g).

(3.16)

Действительный напор, развиваемый колесом, меньше Теоретического при бесконечном количестве лопастей, Н< 1 Ятоо- Это объясняется тем, что, во-первых, часть энергии, (получаемой потоком в межлопастных каналах, затрачива-стся на преодоление гидравлического сопротивления пробочной полости машины (это обстоятельство учитывают ведением в расчет гидравлического КПД Цт, оценивающего совершенство проточной полости машины), и, во-вторых, Сравнение Эйлера (3.8) получено в предположении осевой симметрин потока, т. е. при постоянном осредненном значе-1нии W2 на выходе из межлопастных каналов. Однако в дей-[ствительности скорости W2 распределены по выходному селению рабочего колеса неравномерно, и поэтому переход 1от Ятоо к Ят может быть проведен по формуле

H = liHr, (3.17)

I где ц<1 - поправочный коэффициент, учитывающий ко-нечное число лопастей.

Уравнение Эйлера давало бы точное значение Ят в случае, когда при составлении исходного уравнения (3.2) количество движения потока вычислялось не по среднему значению K2=const, а с учетом действительного распределе-I ния скоростей в выходном сечении колеса.

На основании изложенного вычисление действительно-[го напора ведется по формуле

H = ri,iiHr. (3.18)

Для современных центробежных машин Т1г=0,804-0,96.

Из ряда соотношений для определения поправочного коэффициента j, часто пользуются формулой чешского профессора Стодолы

- sin Рг.

Г - количество лопастей рабочего колеса насоса.

Формула Стодолы дает удовлетворительные практ кие результаты. В ориентировочных расчетах npnHHMaJ ,i 0,8.

3.3. Уравнения энергии потока в рабочем колесе маищ

В машинах, перемещающих газы, p = var и перед! энергии потоку и теплообмен с окружающей средой об, словливает изменение термодинамического состояния г;

Условие сохранения энергии газового потока в рабо] колесе центробежной машины можно записать в виде

где соответственно для входа и выхода рабочего колес и 72 - абсолютные температуры газа; Ci и сг - абсоль скорости; Ср - теплоемкость газа при постоянном давле Lt - удельная энергия, сообщаемая газу; q - количе теплоты, переходящее в окружающую среду, отнесение; 1 кг газа.

Используя (3.7) и вводя поправочный кoэффициet получаем

ц (ыСги - Л ) = (Гг - + + д. (3

oQ Баланс энергии рабочего коле-йентробежной машины

Аналогично (3.20) на основа-нии последнего равенства можно зписать:

, P2 - Pi

(l( 2C2u ~ - -~-

(3.22)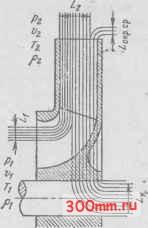

Следовательно, механическая [работа, сообщаемая потоку рабочими лопастями машины, повышает давление в потоке, уве-личивает кинетическую энергию его и отчасти расходуется на преодоление сопротивлений проточной полости.

Рисунок 3.3 дает графическое представление баланса Ьнергии центробежной машины. Здесь обозначено: Li - [удельная энергия потока па входе в рабочее колесо, Дж/кг; ILk -удельная энергия, передаваемая потоку в рабочем [колесе; /-2 - удельная энергия потока на выходе из ра-[бочего колеса; Z-окр.ср - потеря энергии в окружающую [среду.

Это уравнение показывает, что механическая работа, даваемая рабочими лопастями потоку газа, расходуете изменение состояния газа, приращение его кинети ее энергии и частично теряется, переходя в среду, окр жг щую машину, в виде теплоты.

Если машина служит для подачи малосжимаемой кости (насос) или подачи газовой среды при небол! повышении давления (вентилятор), то термодинамич( состояние потока можно полагать неизменяющимся; пература газа в процессе работы машины остается нос ной, и баланс энергии может быть записан так:

где р\ и рг - давление на входе и выходе; h-потерг чг ра в проточной полости машины.

3.4. Влияние угла f2 на напор, развиваемый [центробежной машиной

Влияние угла Рг на примере рабочего колеса с радиаль-1ным входом потока в межлопастные каналы. Из плана скоростей на выходе (см. рис. 3.2) имеем

откуда

2 -C2u=Cjj,ctg(

С2 = 2 -C2rCtgP2.

где -радиальная составляющая абсолютной скорости выходе;

too =