Пусть о - расход через межлопаточные каналы на единице длины отвода, мЗ/(с.м); с - среднее значение тангенциальной составляющей абсолютной скорости на выхо-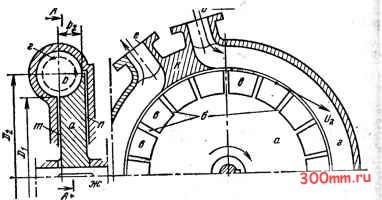

Рис 15 1 Конструктивная схема вихревого насоса:

потока . I

Рис. 15.2. К расчету давления, развиваемого вихревым насосом

де из межлопаточных каналов в отвод, м/с; Со - средняя скорость потока в отводе, м/с.

Если полагать приближенно ось отвода прямолинейной, то по схеме на рис. 15.2 уравнение количества движения для потока, выходящего из колеса в отвод,

~[fp - fiP + Ф)1т = pqdlAtc, - pqdlAtCz.

Следовательно,

(15.1)

Из (15.1) видно, что давление в отводе нарастает в направлении движения пропорционально длине отвода.

Интегрирование (15.1) дает теоретическое повыщение давления на длине I отвода

Рт = Р-у(С2и - Со)1.

Теоретическое повышение напора на длине / отвода

Рт Q.I

, (си-с,). (16.2)

Р8 Sf

Расход в сечении отвода Q=/co, поэтому (15.2.) приводит к следующему уравнению теоретической характеристики вихревого насоса:

(15.3)

Вследствие постоянства q и С2 по длине отвода уравнение (15.3) графически изображается прямой линией (рис. 15.3).

Потери напора в проточной полости насоса пропорциональны квадрату подачи, поэтому, построив на графике на рис. 15.3 характеристики потерь напора /j =mQ вычитанием ординат получаем характеристику действительного напора =/(Q).

Полезная теоретическая мощность вихревого насоса

= PQ,

или, учитывая (15.3),

(15.4)

Это уравнение графически изображается квадратичной параболой с осью, параллельной оси ординат. Очевидно, что jVt=0 при Q=0 Q=fc2n (рис. 15.4).

Максимум Лт находится дифференцированием Лт по Q:

=p4(c.-2f) = 0.

* В основу вывода формулы положена предельно упрощенная модель течения. Действительная картина течения и количественные зависимости чрезвычайно сложны.

Отсюда получим значение Q, при котором достигаете*

(Лт)макС

Максимальное значение по уравнению (15.4)

где m - масса жидкости, проходящей в 1 с через межлс паточные каналы рабочего колеса.

Характеристика Nt=-F{Q) показана иа рис. 15.4.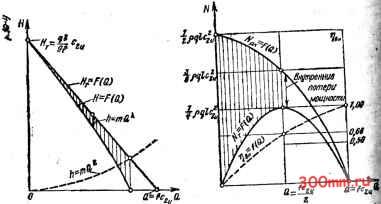

Рис 15 3 Характеристики Рис. 15.4. Характеристики мощно, теоретического дейстни- стей и КПД вихревого насоса тельного напоров вихревого иасоса [к уравнению (15.3)1

Рабочее колесо вихревого насоса увеличивает тангея циальную составляющую скорости жидкости, проходящей через него, от Cq до Сги, составляющая скорости вихревого течения в отводе и рабочем колесе по условию иеразрывйо-сти сохраняется постоянной. Поэтому мощность, затрачиваемую рабочим колесом вихревого иасоса, можно вычислить как разность секундных кинетических энергий потока на выходе и входе:

4и р )

Значения Лр.к дл*я характерных подач, использованных при построении графика Nt=F{Q),

Q = 0; Vp. =

По этим данным построен график Л/p.K = f(Q) (рис. 15.4).

Ввиду того что Л/т - полезная теоретическая мощность, а Np.K - теоретическая мощность, затрачиваемая колесом, внутренний КПД вихревого насоса вычисляется как отношение Nr к Лр.к, определяемое по (15.4) и (15.5),

Окончательное выражение для r]i получается подстановкой в последнее равенство Q=fCo:

(15.6)

Величины 11,- для некоторых значений Q: Q = 0; Со = 0; Лг = 0; Q = fcJ2; Со = cJ2; т) = 0,66;

Q = /C2u;Co = C2 ; TJi = 1.

Характеристика внутреннего КПД показана на рис. 15.4 штриховой линией.

Внутренние потери энергии, обусловленные передачей энергии от рабочего колеса потоку жидкости в отводе, представляются отрезками ординат между кривыми A/p.K=f (Q) и yVT=/(Q).

Из изложенного следует, что при постоянной частоте вращения рабочего колеса внутренние потери энергии в вихревом насосе тем больше, чем меньше подача. Следовательно, эксплуатация вихревого насоса в режиме значительного дросселирования нежелательна.

15.3. Действительные характеристики

Кроме внутренних потерь, свойственных процессу передачи энергии от рабочего колеса потоку в отводе и оцениваемых внутренним КПД но (15.6), в вихревых насосах наблюдаются объемные, гидравлические и- механические по-

тери энергии. Объемные потери энергии здесь значительны! и составляют до 20 % энергии, подводимой к валу вихревого насоса. Они обусловлены перетеканием жидкости через зазоры между поверхностями разделителя к (см. рис* 15.1) и кромками лопастей б рабочего колеса из полости

напорного патрубка в по- ГУ лость всасывания вслед-±1~ ствие неравенства давлений

(Р2>р,).

Гидравлические потер энергии возникают вследст-/о вне трения и вихреобразо-, вания при поступательно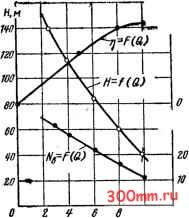

/ff а,л/с

Рис. 15.5. Характеристики вихревого насоса ЭВ-2,7

И циркуляционном движени. 1 ях жидкости в криволинейном отводе вихревого насо-. са. Ввиду того что скорости -этих движений значитель-ны, гидравлические потери . энергии составляют до 30 Yoj энергии иа валу.

Механические потери, как и в центробежных на- сосах, обусловлены трени ем в сальниках и пoдшип:J никах и трением нерабочих поверхностей колеса насоса жидкость в осевых зазорах. Эти потери составляют до 10 % подводимой к насосу энергии.

Столь значительные потери энергии приводят к TOMyjJ что при наиболее благоприятных для вихревых насосо режимах высокой подачи КПД, учитывающий все потер! в лучщих конструкциях, не превышает 0,5.

На рис. 15.5 показаны опытные характеристики вихре вого насоса ЭВ-2,7. Максимум КПД для него составляе всего 32 %.

15.4. Уравновешивание сил, действующих на колесо

Колесо работающего вихревого насоса нагружено про?, дольной й поперечной силами, передающимися на вал.

Продольная сила возникает в результате различия дав- лений на торцовые поверхности колеса в осевых зазорзЗ тип (см. рис. 15.1). Эта сила невелика, легко воспринимается радиальным шариковым подпятником и можех

(рис g применением колеса симметричной формы

Поперечная сила обусловлена тем, что давление в отводе распределяется неравномерно и, как показывают уравнение (15.1) и опыт, пропорционально углу ф (рис. 15.7).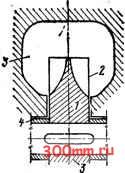

Рис. 15.6. Рабочее колесо с уравновешенной осевой силой:

/ - рабочее колесо с симметричным сечеиием; S - рабочие лопасти; 3 - отвод симметрнчиого сечения; 4 - дистанционные втулки

Рис. 15.7. Распределение давдщия по длине отвода вихревого насоса

Если Я -напор, создаваемый колесом, то давление в произвольном сечении отвода равно Р- ф, его попереч-

ная составляющая равна фзшф.

Элементарная поперечная сила, действующая на длине D ,

отвода -J при ширине колеса В, буДет

В---ф8ШфЙ(р.

Полная поперечная сила п pgHBD

Ф sin фф.