ло изложено в гл. 5, срезаемая стружка сходит по передней поверхности лезвия инструмента под углом к плоскости, перпендикулярной главной режущей кромке в рассматриваемой точке X (направление схода стружки показано стрелками Б на рис. 13.5).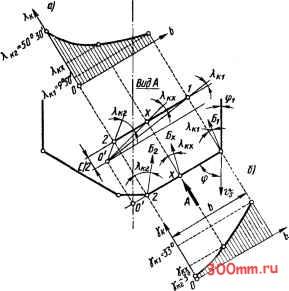

Функции передних поверхностей на зубьях сверл выполняют те участки поверхности винтовых канавок, которые непосредственно примыкают к главным режущим кромкам. Подобно углу наклона главной режущей кромки X передний угол у на чертежах стандартных сверл не указывается и его значение не оговаривается. Значения кинематических передних углов Ук определяются углом наклона со винтовой канавки и, так же как угол X, переменны по текущему радиусу г, точки главной режущей кромки.

На поверхности цилиндра радиусом г, (рис. 13.6) лежит точка х и проходящая через нее винтовая образующая канавки сверла. Шаг винтовой канавки по наружному диаметру сверла L = = nD/tga. Угол со, наклона винтовой образующей поверхности канавки, проходя-

Рис. 13.S

Закономерности изменения углов вдоль главной режущей кромки 1-2 сверла:

о - кинематического угла наклона главной режущей кромки X ; 6 -кинематического переднего угла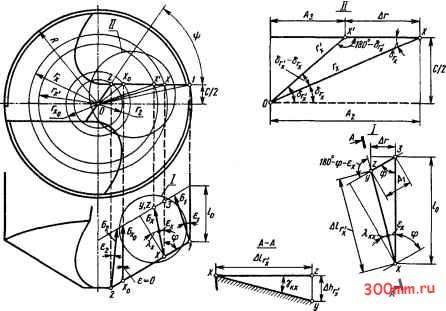

Рис. 13.6. Схема определения кинематического переднего угла винтового сверла

щей через точку х, выражается уравнением (13.4)

tg со, = 2nrJL= 2г tg co/D = tg a/R.

Из рис. 13.6 видно, что стрелка Б, указывающая направление схода стружки, отклоняется от образующей цилиндра радиусом в точке х на угол

(13.5)

где ф - главный угол в плане режущего зуба сверла. В частном случае, когда кинематический угол = 90° - ф, угол Ех=0. В этом случае стрелка Б лежит на образующей цилиндра радиусом г и кинематический передний угол равен углу наклона винтовой образующей канавки в точке Хо, т. е. =

В общем случае стрелка Б отклоняется от образующей цилиндра радиусом и под углом ±£фО пересекает смежные винтовые образующие канавки. В интервале между точками хо и 1 стрелка Б отклоняется влево от образующих щшиндров с радиусами Го < < Г) и угол £ > 0. В сечении А - А, проходящем через стрелку Б, винтовая поверхность канавки пересекается по линии ху. Теоретически эта линия криволинейна, но для малых значений расстояний 1о и А/; (увеличенный участок / на рис. 13.6) ее можно принять за прямую. В сечении А - А линия xz лежит в плоскости, параллельной оси сверла и проходящей через главную режущую кромку 1-2. Примем, что отрезок линии XZ по стрелке Б равен А/,;, а расстояние zy занижения точки у под

плоскостью, в которой лежит линия XZ,

равно Ай;- Тогда угол между линиями XZ и XV с достаточной степенью приближения равен кинематическому переднему углу у исходное уравнение которого имеет вид (13.6)

tgYK.v = Ah,;/A/,..

Точка у лежит на винтовой образующей канавки радиусом г. Развернув винтовую линию ху на плоскость, касательную в точке х к цилиндру радиусом г, получим, как это видно из рис. 13.7,

прямоугольный треугольник, из которого следует, что дуга yz, равная по длине /otgcOri- из-за малости /о может быть также принята за прямую. Из расчетной схемы (рис. 13.7) следует, что

- cos 6 = lo tg COr; cos 6r;.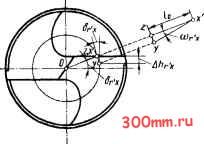

Рис. 13.7. Схема определения занижения точек винтовой канавки сверла

Используя уравнение (13.4), имеем tg со = (2г; tg fo)/D = (ri tg (u)/R,

и тогда (13.7)

Ah = (2/o x tg Ю cos 6r;)/£> = = (ryotgcucos d,.)/R.

Из треугольника хОх (см. увеличенный участок II на рис. 13.6) имеем

rJsin 6,. = Гх/sin 6;,

откуда (13.8)

х = Гх sin Sr/sin 6- и

sin 6, = 0,5c/r = 0,5кП/Гх = kR/r,

где с - толщина перемычки сверла.

Подставив в уравнение (13.8) найденное выражение для sinS, имеем (13.9)

гх = krxR/(rx sin 6,.) = кЯ/sin 6,..

Подставив в формулу (13.7) значение гх из уравнения (13.9), получим

(13.10)

Ай,. = (kRlo tg со cos 6,.)/(Я sin 6,;) = = klo tg co/tg 6,...

Ha торцовой проекции сверла (см.

рис. 13.6) угол 8,; определяет наклон радиуса ri к горизонтальной центровой линии и имеет следующее выражение: (13.11)

tg 8,; = 0,5с/(г, COS 8г - Аг).

Из схемы на горизонтальной проекции сверла (см. увеличенный участок / на рис. 13.6) имеем

Аг = Ai-sin((>;

из косоугольного треугольника xz3 имеем

y4i/sme = /о/8ш(ф +

откуда

Ai =losmeJsm{<p + ex).

Тогда

(13.12)

Аг = Iq sin sin ф/sin (ф + ej.

Подставляя Ar из формулы (13.12) в уравнение (13.11), получаем

(13.13)

kR sin (ф -I- е J

Гх cos 8,. sin (ф -I- - Iq sin sinф

Расстояние A/,; между точками x и z определяется из косоугольного треугольника xz3:

Aljsin ф = /о/sin (ф -I- е),

откуда (13.14)

Al,.. = /о sin ф/sin (ф -I- Ejc).

Подставляя зависимости (13.10) и (13.14) в формулу (13.6), находим

tg Ykx = tg ю sin (ф -I- e)/(sin ф tg 8,).

Заменив tg6r; его выражением по уравнению (13.13), получаем общее выражение кинематического переднего угла у сверл: (13.15)

г = kR sin ф/sin Ко = IR sin 587sin 32° = = 1,6 kR.

Эпюра изменения переднего кинематического угла укх показана на рис. 13.5, б.

Задний угол сх проставляется на чф-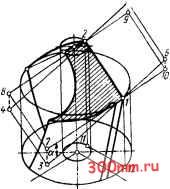

Рис. 13.8. Схема образования заднего угла а при плоскостной заточке винтовых сверл

тежах сверл лишь в тех случаях, когда задние поверхности на зубьях затачиваются по плоскостям. На рис. 13.8 заштрихована заточенная по плоскости 3-4-5-6 задняя поверхность зуба сверла. Показанная на рис. 13.8 плоскость 7-8-9-10 перпендикулярна плоскости 1-2-11-12, параллельной оси сверла и проходящей через главную режущую кромку 1-2. Таким образом, главная режущая кромка 1-2 является линией пересечения всех трех плоскостей. Значение затачиваемого заднего угла сх определяется углом между двумя плоскостями - плоскостью 3-4-5-6 и плоскостью 7-8-9-10 - и постоянно вдоль всей режущей кромки 1-2. На чертежах, по которым изготовляют инструмент, задний угол

tov tgю[гхcos6,sin(ф -Н eJ - /р sinsinф]

КвШф

У стандартных сверл, имеющих главный задается в плоскости, перпендикулярной угол в плане ф = 58°, при Х = 32° угол главной режущей кромке. При заточ-Ejc = О, а радиус ке сверл на специальных сверлозаточ-