ВЫСОКОГО порядка, чем квадратичная. Несмотря на то что интерполяция высокого порядка обеспечивает большую точность, она приводит к системам уравнений, содержащим намного больше ненулевых членов, чем при использовании интерполяции низкого порядка; следовательно, интерполяция высокого порядка является более дорогостоящей в вычислительном отношении, особенно при двух или трех измерениях. Достижение надлежащего баланса между точностью и экономичностью, т. е. выбор методов обладающих вычислительной эффективностью (см. § 4.5), является одной из наиболее интересных стратегических особенностей вычислительной гидроаэродинамики.

При измельчении сетки мы вправе ожидать, что ошибка конечно-элементного решения будет уменьшаться с такой же скоростью, что и интерполяционная ошибка. В общем случае при заданной сетке ошибка решения будет больше, так как она включает и дополнительную ошибку, обусловленную тем, что решение в узловой точке не совпадает с точным решением. Грубо говоря, применение линейных аппроксимирующих функций приводит к решениям, обладающим примерно такой же точностью, что и решения, построенные с помощью конечно-разностных методов второго порядка, тогда как применение квадратичных аппроксимирующих функций приводит примерно к такой же точности, что и применение конечно-разностных методов третьего порядка.

5.3.3, Двумерная интерполяция

Понятие конечных элементов, давшее название самому методу, становится более полезным, если число измерений превышает единицу. Так, при двух измерениях локальное решение интерполируется по отдельности внутри каждого из четырех элементов Л, В, С и D, окружающих узел (/, k) (рис. 5.11). Приближенное решение, эквивалентное выражению (5.44), весьма удобно представляется с помощью введения координатной системы (g, т]), привязанной к элементу. При билинейной интерполяции приближенное решение можно записать в виде

T=tTih{l. л), (5.58)

где для каждого элемента -1 1, -1 т] 1 (см. рис. 5.11). Согласно выражению (5.58), в каждый элемент вносят свои вклады по четыре члена. Аппроксимирующая функция </(, г) приобретает форму

ф1 (g, Tl) = 0.25 (1 + hi) (1 + Л/Л). (5.59)

(5.60)

Например, внутри элемента С, показанного на рис. 5.15, имеем

, = 0.25(1-)(1-л).

2 = 0.25(1+)(1-т1),

3 = 0.25(1+g)(l+ti).

4 = 0.25(1-5) (I+Ti).

откуда следует, что Ф1 = I при 1 = Ь> л = Л/ и ф1 = 0 во всех остальных узлах. На линиях постоянного или т) аппроксими-

h+l 4=1

Рис 5.11. Глобальная и локальная нумерация узлов.

рующие функции Ф1 обнаруживают такой же характер изменения, как и одномерные аппроксимирующие функции (см. рис. 5.8).

Трехмерное изображение билинейной интерполяционной функции, центрированной в узле (/, k), показано на рис. 5.12. Рассматривая выражение (5.58) и рис. 5.12, можно убедиться, что функция Т остается непрерывной при пересечении границ элементов; однако это не так по отношению к производным Г.

Как и в одномерном случае, внутри каждого конкретного элемента можно определить двумерные биквадратные интерполяционные функции (рис. 5.13). Для лагранжевых элементов приближенное решение, эквивалентное выражению (5.44), принимает форму

(5.61)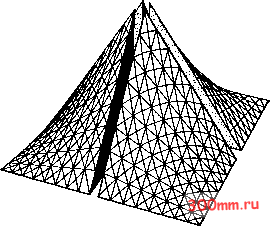

Рис. 5.12. Билинейная интерполяционная функция.

Рис. 5.13. Двумерные квадратичные элементы Лагранжа.